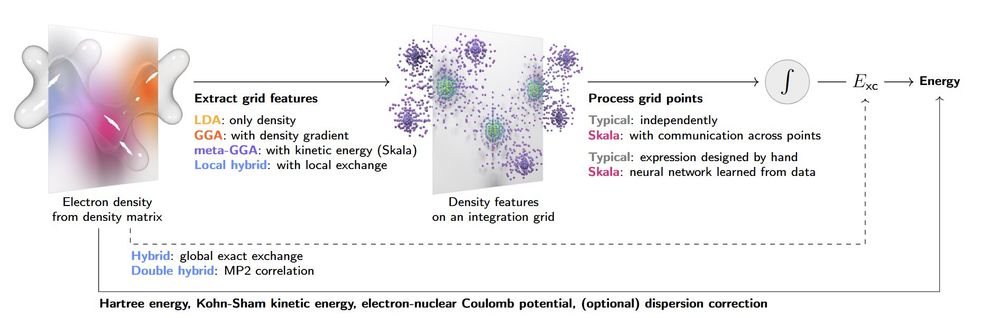
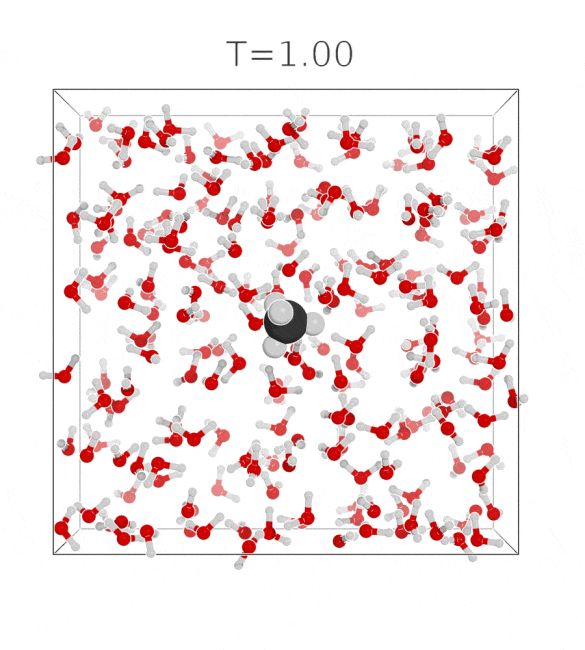
Bálint Máté
@balintmate.bsky.social
54 followers
75 following
10 posts
phd student @geneva, ML+physics
https://balintmate.github.io
Posts
Media
Videos
Starter Packs
Reposted by Bálint Máté
Bálint Máté
@balintmate.bsky.social
· Dec 17
Bálint Máté
@balintmate.bsky.social
· Dec 17
Bálint Máté
@balintmate.bsky.social
· Dec 17