Thanks so much to my co-authors Weijie Xiong @qzoeholmes.bsky.social @aangrisani.bsky.social Yudai Suzuki @thipchotibut.bsky.social It's real fun to work with you all 😃🙌

Also, special thanks to @mvscerezo.bsky.social Martin Larocca for their valuable insight on correlated Haar random unitaries 🌮

So yes, big question for future QRP design: how to pick your circuit depth or interaction time so that you remain powerful without going full random.

You want that “just right” level of chaos: enough to get expressive states, not so much that it all washes out.

Episode 4: New Hope

Not everything is gloom and doom. We found that for moderate scrambling (like shallow random circuits or chaotic Ising with short evolution), you don’t get lethal exponential concentration.

Episode 3: Noise erases memo...

We also studied QRP under local unital or non-unital noise. While there are work that argue dissipation as a resource for QRP, we prove noise also forces your reservoir to forget states from the distant past exponentially quickly

Episode 2: Oh what ! I forgot now

We prove that in extreme-scrambling QRPs, old inputs or initial states get forgotten exponentially fast (in both time steps and system size !). Too much scrambling -> you effectively “MIB” zap each past input.

Hence our new results show that, while chaotic (extreme-scrambling) reservoirs are fine for processing information in small setups as people have studied, they suffer from scalability issue to larger models doomed by their own chaoticity.

Episode 1: Scalability barrier

Based on the unrolled form, we prove the exponential concentration of QRP output. In a large scale setting, the trained QRP model becomes input-insensitive leading to poor generalization despite trainability guarantee.

To address this challenge, we apply tensor-diagram approaches to unroll multi-step QRP into a single high-moment Haar integral on a larger dimension amenable for scalability and memory analysis.

Episode 0: Temporal correlation hinders standard analytical techniques.

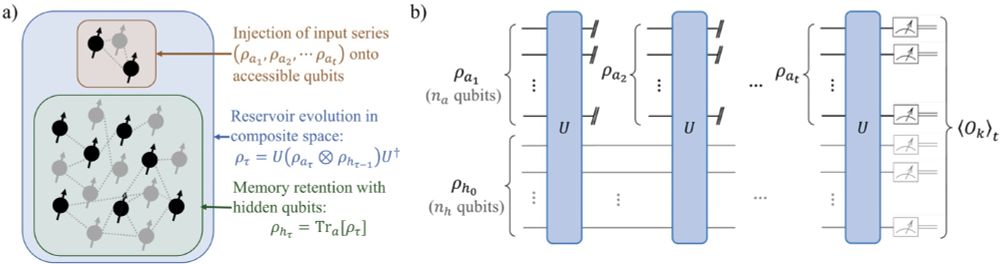
While related techniques already establish scalability barriers for other quantum models, the QRP protocol is much more demanding: a fixed reservoir repeatedly interleaves with a stream of input time-series.

Our key messages can be summarized as

🎯 Big scrambling in quantum reservoirs helps at small sizes but kills input-sensitivity at large scale
🎯 Memory of older states decays exponentially (in both time steps and system size !)
🎯 Noise can make us forget even faster

The QRP model processes input time series of quantum states. Here we model the extreme scrambling reservoir as an instance drawn from a high-order design unitary ensemble.