https://cs.smith.edu/~jorourke/
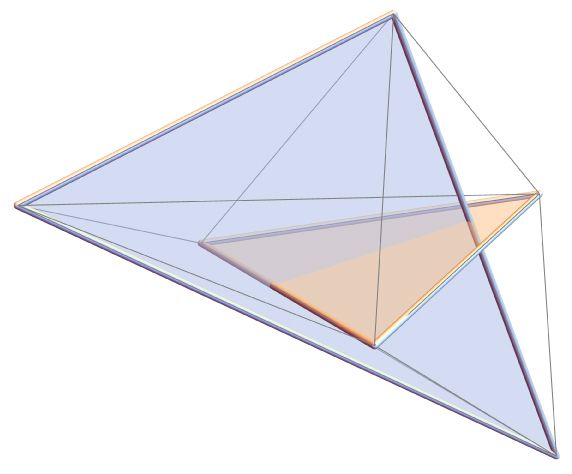
Polyhedron displayed in banner has max volume of all foldings from a square.
#MathSky #MathArt #Geometry #Origami
More examples: erikdemaine.org/curved/)

#MathSky #MathArt #Geometry #Origami
More examples: erikdemaine.org/curved/)
Expected online publication date: December 2025. Print publication: 31 December 2025.
www.science.smith.edu/~jorourke/Ma...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt

Expected online publication date: December 2025. Print publication: 31 December 2025.
www.science.smith.edu/~jorourke/Ma...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt

gwtokarsky.github.io. #MathSky #Mathematics #Geometry #Billiards

gwtokarsky.github.io. #MathSky #Mathematics #Geometry #Billiards
doi.org/10.1007/s004...
#MathSky #Mathematics #Geometry #Polyhedra

doi.org/10.1007/s004...
#MathSky #Mathematics #Geometry #Polyhedra
#MathSky #Mathematics #Geometry #Probability

#MathSky #Mathematics #Geometry #Probability
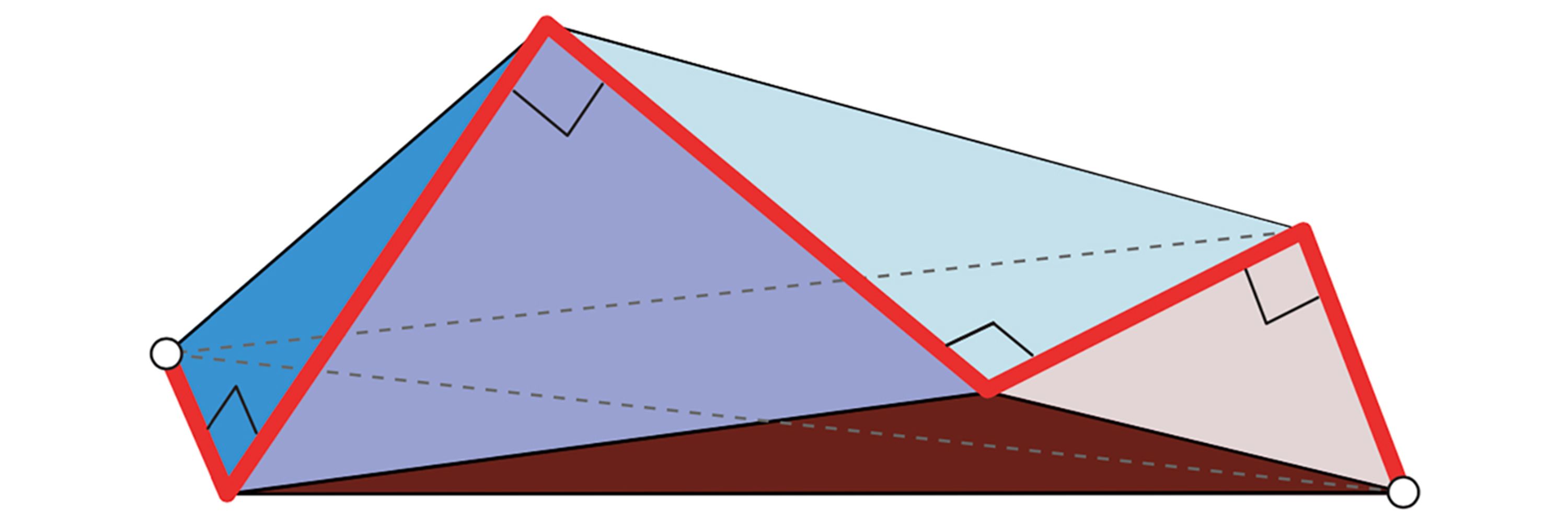
Each unit square includes a circular arc of a 1/2-radius circle centered at each vertex.
Adams, Colin. "Spandrelized Tilings." Amer. Math. Monthly 132, no. 3 (2025): 199-217.
doi.org/10.1080/0002...
#MathSky #Mathematics #Geometry #Tiling

Each unit square includes a circular arc of a 1/2-radius circle centered at each vertex.
Adams, Colin. "Spandrelized Tilings." Amer. Math. Monthly 132, no. 3 (2025): 199-217.
doi.org/10.1080/0002...
#MathSky #Mathematics #Geometry #Tiling
#Mathematics #MathSky #Geometry

#Mathematics #MathSky #Geometry
arxiv.org/abs/2509.07906
#MathSky #Mathematics #Geometry #Tiling

arxiv.org/abs/2509.07906
#MathSky #Mathematics #Geometry #Tiling
(doi.org/10.1016/j.ms...)
Here I show a hexagonal design built with origami waterbomb crease patterns.
cs.smith.edu/~jorourke/Ma...
#Mathematics #Geometry #MathSky

(doi.org/10.1016/j.ms...)
Here I show a hexagonal design built with origami waterbomb crease patterns.
cs.smith.edu/~jorourke/Ma...
#Mathematics #Geometry #MathSky
arxiv.org/abs/2508.18475
#Mathematics #Geometry #MathSky
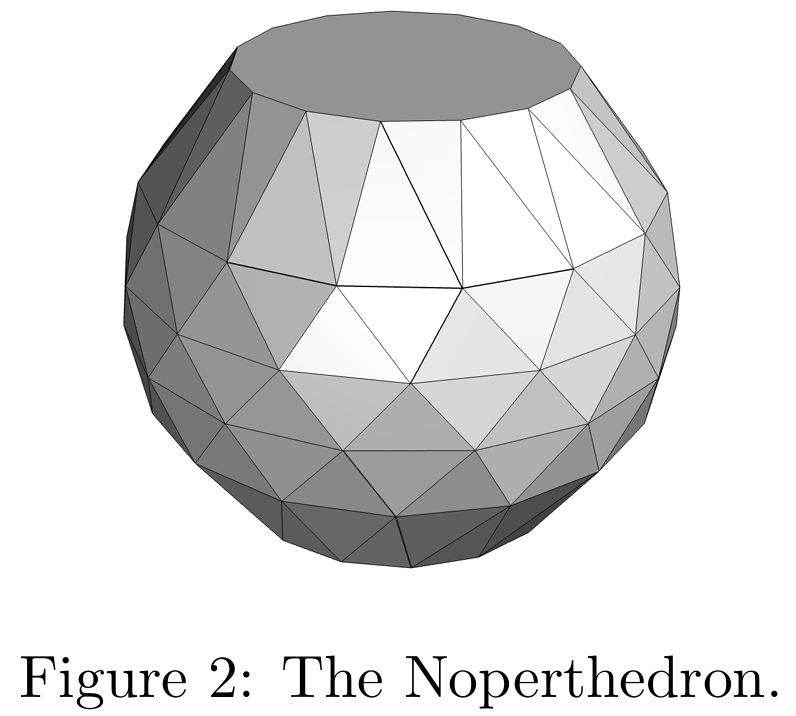
arxiv.org/abs/2508.18475
#Mathematics #Geometry #MathSky
#MathSky #Geometry #Mathematics
#MathSky #Geometry #Mathematics


en.wikipedia.org/wiki/Saturn%...
#MathSky #Geometry #Astronomy #Planets

en.wikipedia.org/wiki/Saturn%...
#MathSky #Geometry #Astronomy #Planets
(en.wikipedia.org/wiki/Stanfor...)
Developed by Stanford researchers in 1994
as a test bed model for computer graphics algorithms. This version: 2,503 vertices.
#MathSky #Geometry #Graphics

(en.wikipedia.org/wiki/Stanfor...)
Developed by Stanford researchers in 1994
as a test bed model for computer graphics algorithms. This version: 2,503 vertices.
#MathSky #Geometry #Graphics
(en.wikipedia.org/wiki/Prince_...)
#MathSky #Geometry
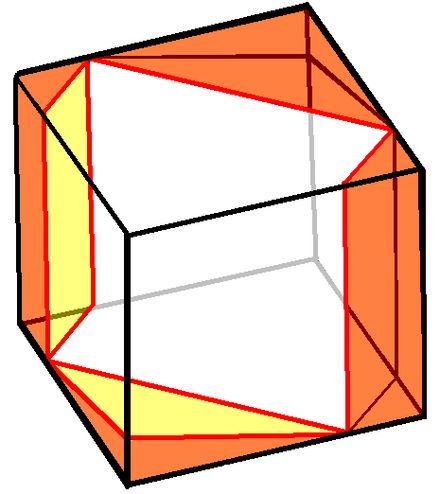
(en.wikipedia.org/wiki/Prince_...)
#MathSky #Geometry


#MathSky
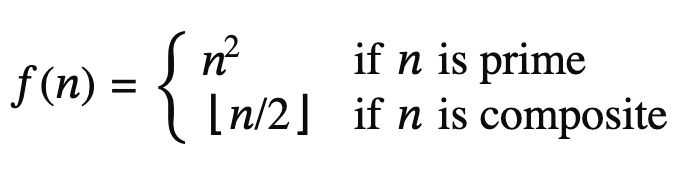
#MathSky