Alumni: University of Coimbra · Charles University in Prague


My name is Viktor, and having been frustrated by the countless hours I spent studying and deciphering math from long, linear, exhausting paragraphs of text, I am now pioneering spatial writing to make studying and reading much friendlier for our brains.
+2𝑔𝑛 - shift of homology degree coming from:
2 - full twist
𝑔 - number of negative twists in 𝑋
𝑛 - number of free strands
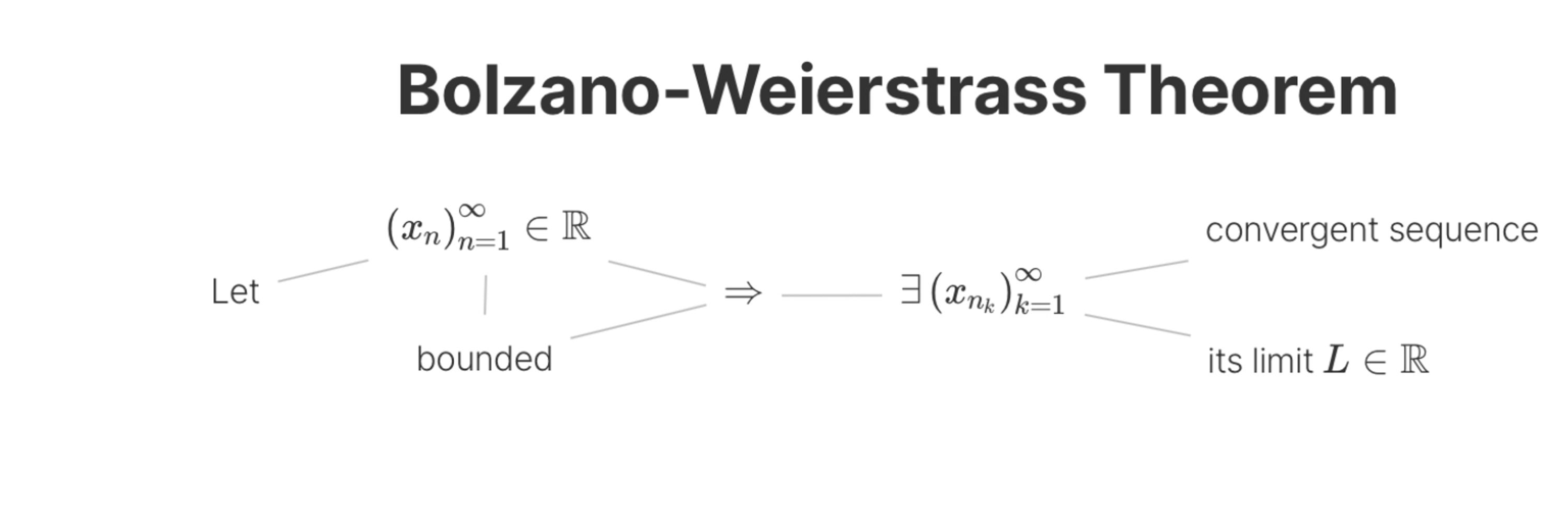
Read the spatial story:
brainec.com/s/oc82wP8HXxMUMTkZ3dlU
Based on van den Berg et al. (2015), Braid Floer Homology.

+2𝑔𝑛 - shift of homology degree coming from:
2 - full twist
𝑔 - number of negative twists in 𝑋
𝑛 - number of free strands
Read the spatial story:
brainec.com/s/oc82wP8HXxMUMTkZ3dlU
Based on van den Berg et al. (2015), Braid Floer Homology.
𝑠𝑡𝑟𝑎𝑛𝑑 - 1-dimensional curve (in 𝑆¹×𝐷²)
𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 - only positive crossings (strand 𝑖 passes over 𝑖+1)
[𝑋 rel 𝑌] - relative braid class (𝑋 - free strands that twist around 𝑌 - fixed strands)
[𝑋₊ rel 𝑌₊] - positive rel. braid class (𝑋₊ -||- that twist *positively* around 𝑌₊)
𝑠𝑡𝑟𝑎𝑛𝑑 - 1-dimensional curve (in 𝑆¹×𝐷²)
𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 - only positive crossings (strand 𝑖 passes over 𝑖+1)
[𝑋 rel 𝑌] - relative braid class (𝑋 - free strands that twist around 𝑌 - fixed strands)
[𝑋₊ rel 𝑌₊] - positive rel. braid class (𝑋₊ -||- that twist *positively* around 𝑌₊)
"Positive braids realize, up to shifts, all possible Braid-Floer homologies"
HB*([𝑋 rel 𝑌]) ≅ HB*+2𝑔𝑛([𝑋₊ rel 𝑌₊])
= "Braid-Floer homology of relative braid class is isomorphic to shifted Braid-Floer homology of positive relative braid class"
"Positive braids realize, up to shifts, all possible Braid-Floer homologies"
HB*([𝑋 rel 𝑌]) ≅ HB*+2𝑔𝑛([𝑋₊ rel 𝑌₊])
= "Braid-Floer homology of relative braid class is isomorphic to shifted Braid-Floer homology of positive relative braid class"
If there are no images, only math expressions and text, it runs fully offline.
Image embedding for offline use is in development.
If there are no images, only math expressions and text, it runs fully offline.
Image embedding for offline use is in development.
Linear text is infected with AI, but spatial text forces the author to write and to understand what they are writing.
Guess which campus did I visit yesterday!


Linear text is infected with AI, but spatial text forces the author to write and to understand what they are writing.
Guess which campus did I visit yesterday!


Guess which campus did I visit yesterday!
My pleasure to connect, always 🎩
MSc Thesis: hdl.handle.net/10316/96137
My pleasure to connect, always 🎩
MSc Thesis: hdl.handle.net/10316/96137
I've been working on this interdisciplinary vision of spatial writing that intertwines interaction design, comp. sci., cognitive science... ↓
I've been working on this interdisciplinary vision of spatial writing that intertwines interaction design, comp. sci., cognitive science... ↓
𝐋𝐞𝐦𝐦𝐚 𝟒.𝟒. (𝐃𝐞𝐧𝐬𝐢𝐭𝐲-𝐨𝐧𝐞 𝐃𝐚𝐯𝐢𝐬–𝐋𝐞𝐥𝐢𝐞̀𝐯𝐫𝐞)
brainec.com/s/PCIEHHEEPE...
Based on: Kontorovich, A., & Zhang, X. (2024). On the local-global conj... arXiv:2409.10682

𝐋𝐞𝐦𝐦𝐚 𝟒.𝟒. (𝐃𝐞𝐧𝐬𝐢𝐭𝐲-𝐨𝐧𝐞 𝐃𝐚𝐯𝐢𝐬–𝐋𝐞𝐥𝐢𝐞̀𝐯𝐫𝐞)
brainec.com/s/PCIEHHEEPE...
Based on: Kontorovich, A., & Zhang, X. (2024). On the local-global conj... arXiv:2409.10682
brainec.com/s/ZmkrjF2ml2...

brainec.com/s/ZmkrjF2ml2...
In 1737 Euler showed that Σ 1/𝑝 diverges.
In 1874 Mertens’ Second Theorem estimated how quickly.
The growth is very slow: log log 𝑥.
For 𝑥 ∈ ℝ, 𝑝 prime and 𝑥 ≥ 2:
Σₚ≤𝑥 1/𝑝 = log log 𝑥 + 𝑀 + O(1/log 𝑥)
Meissel-Mertens constant
𝑀 ≈ 0.26149721…
#Math #NumberTheory
In 1737 Euler showed that Σ 1/𝑝 diverges.
In 1874 Mertens’ Second Theorem estimated how quickly.
The growth is very slow: log log 𝑥.
For 𝑥 ∈ ℝ, 𝑝 prime and 𝑥 ≥ 2:
Σₚ≤𝑥 1/𝑝 = log log 𝑥 + 𝑀 + O(1/log 𝑥)
Meissel-Mertens constant
𝑀 ≈ 0.26149721…
#Math #NumberTheory
www.brainec.com/s/UlzYMrr8rO...

www.brainec.com/s/UlzYMrr8rO...
φ(𝑛) = how many positive integers ≤ than 𝑛 are relatively prime to 𝑛
φ(𝑛) = |{ 𝑘 ∈ ℕ : 𝑘 ≤ 𝑛, gcd(𝑘,𝑛)=1 }|
𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑒𝑙𝑦 𝑝𝑟𝑖𝑚𝑒 ≡ 𝑐𝑜𝑝𝑟𝑖𝑚𝑒 ≡ gcd(𝑎,𝑏)=1
𝑬𝒙𝒂𝒎𝒑𝒍𝒆:
φ(9) = 6
{1,2,4,5,7,8}
#math #NumberTheory
φ(𝑛) = how many positive integers ≤ than 𝑛 are relatively prime to 𝑛
φ(𝑛) = |{ 𝑘 ∈ ℕ : 𝑘 ≤ 𝑛, gcd(𝑘,𝑛)=1 }|
𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑒𝑙𝑦 𝑝𝑟𝑖𝑚𝑒 ≡ 𝑐𝑜𝑝𝑟𝑖𝑚𝑒 ≡ gcd(𝑎,𝑏)=1
𝑬𝒙𝒂𝒎𝒑𝒍𝒆:
φ(9) = 6
{1,2,4,5,7,8}
#math #NumberTheory
www.brainec.com/s/2SIKNGSmeF...

www.brainec.com/s/2SIKNGSmeF...
Precursor of the Prime Number Theorem
For 𝑥 ∈ ℝ and 𝑥 ≥ 2:
∏ₚ≤𝑥 (1 − 1/𝑝) = e⁻ᵞ(1+o(1))/ln𝑥
Euler–Mascheroni constant
γ ≈ 0.57721566…
#math #NumberTheory
Precursor of the Prime Number Theorem
For 𝑥 ∈ ℝ and 𝑥 ≥ 2:
∏ₚ≤𝑥 (1 − 1/𝑝) = e⁻ᵞ(1+o(1))/ln𝑥
Euler–Mascheroni constant
γ ≈ 0.57721566…
#math #NumberTheory

Also called = Taylor/Maclaurin expansion of ln(1+𝑥)
If |𝑥|<1 then:
ln(1+𝑥) = Σₙ₌₁ (−1)ⁿ⁺¹ 𝑥ⁿ/𝑛
ln(1+𝑥) = 𝑥 − 𝑥²⁄2 + 𝑥³⁄3 − 𝑥⁴⁄4 + …
#mathematics #RealAnalysis
Also called = Taylor/Maclaurin expansion of ln(1+𝑥)
If |𝑥|<1 then:
ln(1+𝑥) = Σₙ₌₁ (−1)ⁿ⁺¹ 𝑥ⁿ/𝑛
ln(1+𝑥) = 𝑥 − 𝑥²⁄2 + 𝑥³⁄3 − 𝑥⁴⁄4 + …
#mathematics #RealAnalysis

Core identity in analytic number theory linking Dirichlet series to primes
If 𝑓 is multiplicative & series converges absolutely at 𝑠:
∑ₙ 𝑓(𝑛)/𝑛ˢ = ∏ₚ ( ∑ₖ 𝑓(𝑝ᵏ)/𝑝ᵏˢ )
“sum over all integers” = “product over primes” (one sum per prime)
#mathematics #NumberTheory
Core identity in analytic number theory linking Dirichlet series to primes
If 𝑓 is multiplicative & series converges absolutely at 𝑠:
∑ₙ 𝑓(𝑛)/𝑛ˢ = ∏ₚ ( ∑ₖ 𝑓(𝑝ᵏ)/𝑝ᵏˢ )
“sum over all integers” = “product over primes” (one sum per prime)
#mathematics #NumberTheory
- estimating sums of arithmetic functions
- discrete “integration by parts” for sums
- transforming hard sums into easier integrals
Read the spatial story:
www.brainec.com/s/SXxDYUDZPw...

- estimating sums of arithmetic functions
- discrete “integration by parts” for sums
- transforming hard sums into easier integrals
Read the spatial story:
www.brainec.com/s/SXxDYUDZPw...
shows how a weighted sum (by 𝑓) can be expressed using cumulative sum (𝐴(𝑥)) and the way function 𝑓 changes
If 𝑓:[1,𝑁]⟼ℂ continuously differentiable & 𝐴(𝑥) = Σₙ≤𝑥 𝑎ₙ:
Σₙ₌₁ᴺ 𝑎ₙ 𝑓(𝑛) = 𝐴(𝑁) 𝑓(𝑁) − ∫₁ᴺ 𝐴(𝑥) 𝑓′(𝑥) d𝑥
Used for: ↓
shows how a weighted sum (by 𝑓) can be expressed using cumulative sum (𝐴(𝑥)) and the way function 𝑓 changes
If 𝑓:[1,𝑁]⟼ℂ continuously differentiable & 𝐴(𝑥) = Σₙ≤𝑥 𝑎ₙ:
Σₙ₌₁ᴺ 𝑎ₙ 𝑓(𝑛) = 𝐴(𝑁) 𝑓(𝑁) − ∫₁ᴺ 𝐴(𝑥) 𝑓′(𝑥) d𝑥
Used for: ↓
www.brainec.com/s/PCIEHHEEPE...

www.brainec.com/s/PCIEHHEEPE...
𝑓(𝑛) = 1 - if 𝑛 squarefree, 𝑓(𝑛) = 0 otherwise
𝑁𝑜𝑡𝑖𝑐𝑒: multiplying a non-squarefree number by any squarefree number always gives a non-squarefree number.
Read the short spatial story: www.brainec.com/s/HO31YvCkft...

𝑓(𝑛) = 1 - if 𝑛 squarefree, 𝑓(𝑛) = 0 otherwise
𝑁𝑜𝑡𝑖𝑐𝑒: multiplying a non-squarefree number by any squarefree number always gives a non-squarefree number.
Read the short spatial story: www.brainec.com/s/HO31YvCkft...

