



1/3 🌊 Measuring experimentally the dispersion of #microplastic #fibres in turbulent flows is incredibly challenging, due to their small size. However, experiments are key to develop reliable models to predict the fate of microplastics in #environmental #flows.
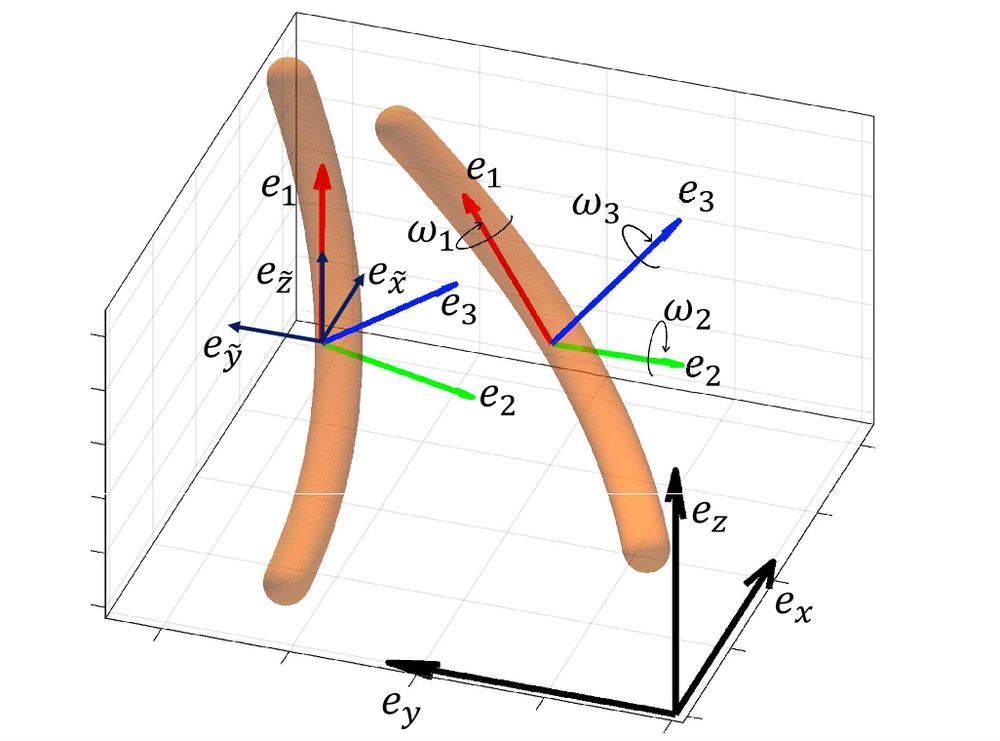
1/3 🌊 Measuring experimentally the dispersion of #microplastic #fibres in turbulent flows is incredibly challenging, due to their small size. However, experiments are key to develop reliable models to predict the fate of microplastics in #environmental #flows.
📕 Paper agupubs.onlinelibrary.wiley.com/doi/10.1029/...
💻 Data figshare.com/articles/dat...
#PhysicsOfFluids #physics #engineering #OpenAccess #OpenSource #UniversityTwente #TUWien

📕 Paper agupubs.onlinelibrary.wiley.com/doi/10.1029/...
💻 Data figshare.com/articles/dat...
#PhysicsOfFluids #physics #engineering #OpenAccess #OpenSource #UniversityTwente #TUWien
And there is no doubt about that.
But what will it happen in the subsurface?
agupubs.onlinelibrary.wiley.com/doi/10.1029/...

And there is no doubt about that.
But what will it happen in the subsurface?
agupubs.onlinelibrary.wiley.com/doi/10.1029/...

🧵1/6 We present the code AFiD-Darcy, designed for massively parallel numerical simulations of convective porous media flows. Thanks to Guru Sreevanshu Yerragolam, Detlef Lohse and Roberto Verzicco for the great collaboration at @poftwente.bsky.social
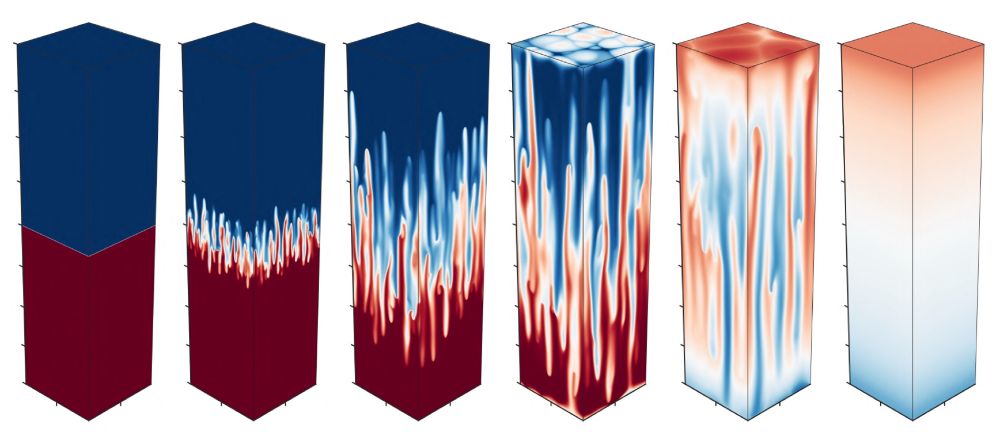
🧵1/6 We present the code AFiD-Darcy, designed for massively parallel numerical simulations of convective porous media flows. Thanks to Guru Sreevanshu Yerragolam, Detlef Lohse and Roberto Verzicco for the great collaboration at @poftwente.bsky.social
cocalc.com/Cambridge/S0...
cocalc.com/Cambridge/S0...

Congratulations also to the promotion team: Detlef Lohse and Roberto Verzicco. #FluidDynamics #particles


Congratulations also to the promotion team: Detlef Lohse and Roberto Verzicco. #FluidDynamics #particles
www.annualreviews.org/content/jour...


www.annualreviews.org/content/jour...


www.annualreviews.org/content/jour...
arXiv: tinyurl.com/2c7v7lzc.
Video: tinyurl.com/2crhbjtp
arXiv: tinyurl.com/2c7v7lzc.
Video: tinyurl.com/2crhbjtp



