
Lover of Linux 🐧, coffee ☕, and retro gaming. Big fan of open-source. #gohabsgo 🇨🇦
For more info: https://linktr.ee/sharky6000

Code World Models for General Game-Playing. ♟️🎲 ♣️♥️♠️♦️
I am pleased to announce our new paper, which provides an extremely sample-efficient way to create an agent that can perform well in multi-agent, partially-observed, symbolic environments!
🧵 1/N

@euripsconf.bsky.social too.)
TL;DR: Coupling obs and agent IDs can hurt performance in MARL. Agent-conditioned hypernets cleanly decouple grads and enable specialisation.
📜: arxiv.org/abs/2412.04233

@euripsconf.bsky.social too.)
TL;DR: Coupling obs and agent IDs can hurt performance in MARL. Agent-conditioned hypernets cleanly decouple grads and enable specialisation.
📜: arxiv.org/abs/2412.04233
On emotions and value functions: youtu.be/aR20FWCCjAs?...

On emotions and value functions: youtu.be/aR20FWCCjAs?...
youtu.be/aR20FWCCjAs?...

youtu.be/aR20FWCCjAs?...
Why the heck am I hearing this for the first time in late 2025?
Why the heck am I hearing this for the first time in late 2025?
We introduce MMBench: a 200-task RL benchmark, and Newt: a language-conditioned multitask world model trained with large-scale online RL.
www.nicklashansen.com/NewtWM/
Code, checkpoints, dataset etc. are open-source!
We introduce MMBench: a 200-task RL benchmark, and Newt: a language-conditioned multitask world model trained with large-scale online RL.
www.nicklashansen.com/NewtWM/
Code, checkpoints, dataset etc. are open-source!
🎬 This is a new, HTML-based submission format for TMLR, that supports interactive figures and videos, along with the usual LaTeX and images.
🎉 Thanks to TMLR Editors in Chief: Hugo Larochelle, @gautamkamath.com, Naila Murray, Nihar B. Shah, and Laurent Charlin!
🎬 This is a new, HTML-based submission format for TMLR, that supports interactive figures and videos, along with the usual LaTeX and images.
🎉 Thanks to TMLR Editors in Chief: Hugo Larochelle, @gautamkamath.com, Naila Murray, Nihar B. Shah, and Laurent Charlin!
Thanks to Paul Vicol (@paulvicol.bsky.social) for his tireless work on this new option, as well as the OpenReview team.
🎬 This is a new, HTML-based submission format for TMLR, that supports interactive figures and videos, along with the usual LaTeX and images.
🎉 Thanks to TMLR Editors in Chief: Hugo Larochelle, @gautamkamath.com, Naila Murray, Nihar B. Shah, and Laurent Charlin!
Thanks to Paul Vicol (@paulvicol.bsky.social) for his tireless work on this new option, as well as the OpenReview team.
It brings me back to the good ol' days .. late 90's / early 2000s when I first go into EDM. I'd listen to this kind of stuff for hours.
Anybody see this song played live?
And I think it's a reference to.. 👇
youtu.be/degq0sxYlLI?...

It brings me back to the good ol' days .. late 90's / early 2000s when I first go into EDM. I'd listen to this kind of stuff for hours.
Anybody see this song played live?
And I think it's a reference to.. 👇
youtu.be/degq0sxYlLI?...
Just watch it, it's great!
Just watch it, it's great!
X quietly disabled a new feature that showed which country an account was posting from when it revealed that lots of popular right wing MAGA accounts were being run from foreign countries like India and Nigeria.


X quietly disabled a new feature that showed which country an account was posting from when it revealed that lots of popular right wing MAGA accounts were being run from foreign countries like India and Nigeria.


I always wanted to create a nice Gemma timeline for my presentations but I'm not that good with drawing tools
With just one prompt I managed to create something pretty cool!!
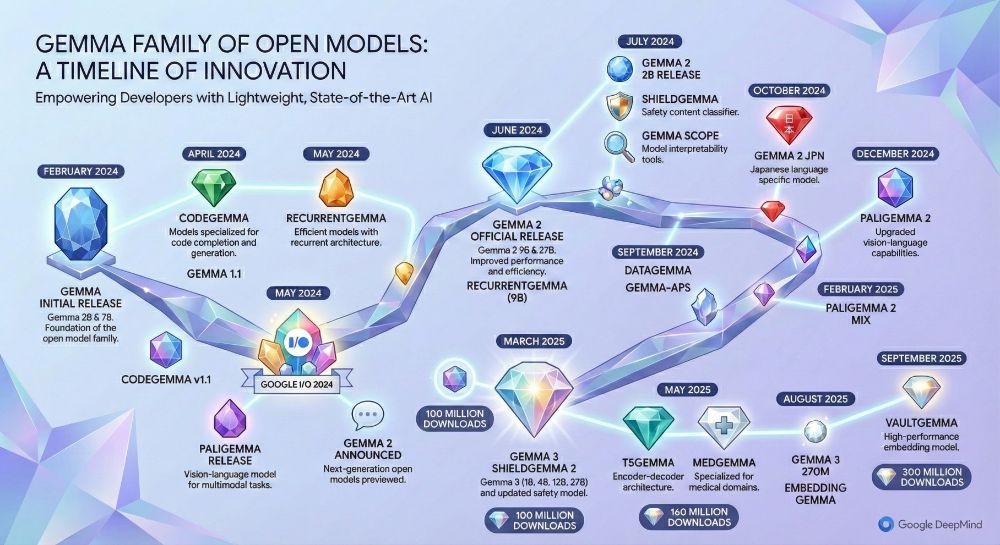
I always wanted to create a nice Gemma timeline for my presentations but I'm not that good with drawing tools
With just one prompt I managed to create something pretty cool!!


- Theory of MARL: experience with theory and/or MARL
-Formal methods for MARL: experience with formal methods or MARL (interest in learning the other)
www.khoury.northeastern.edu/programs/com...

- Theory of MARL: experience with theory and/or MARL
-Formal methods for MARL: experience with formal methods or MARL (interest in learning the other)
www.khoury.northeastern.edu/programs/com...
blog.google/products/gem...
Gemini 3 performs quite well on a wide range of benchmarks.

blog.google/products/gem...
Gemini 3 performs quite well on a wide range of benchmarks.

Combined with its advanced understanding of the real world, Gemini 3 Pro is our most intelligent model for building complex apps.
goo.gle/43ADuV6

Combined with its advanced understanding of the real world, Gemini 3 Pro is our most intelligent model for building complex apps.
goo.gle/43ADuV6




