

But in fact the AM-GM inequality, just for ℕ, can be stated purely using ℕ (clear denoms, raise everything to n'th power). Is there a simple proof avoiding ℝ?
But in fact the AM-GM inequality, just for ℕ, can be stated purely using ℕ (clear denoms, raise everything to n'th power). Is there a simple proof avoiding ℝ?
A chat around what's been happening in the world of AI and Erdos problems, and what it highlights.

A chat around what's been happening in the world of AI and Erdos problems, and what it highlights.



www.scientificamerican.com/article/math...

www.scientificamerican.com/article/math...
www.nsf.gov/news/nsf-inv...

www.nsf.gov/news/nsf-inv...

1) It will create a hard dataset for autoformalization AI's;
2) It will force us to formalize the definitions of mathematical objects which are being used today in the top journals, thus making Lean's mathematics library more relevant to modern math researchers.
www.imperial.ac.uk/jobs/search-...
Positions are for 2 years, start date 1st Oct this year. Deadline 15th August.

1) It will create a hard dataset for autoformalization AI's;
2) It will force us to formalize the definitions of mathematical objects which are being used today in the top journals, thus making Lean's mathematics library more relevant to modern math researchers.
www.imperial.ac.uk/jobs/search-...
Positions are for 2 years, start date 1st Oct this year. Deadline 15th August.

www.imperial.ac.uk/jobs/search-...
Positions are for 2 years, start date 1st Oct this year. Deadline 15th August.
www.renaissancephilanthropy.org/news-and-ins...

www.renaissancephilanthropy.org/news-and-ins...

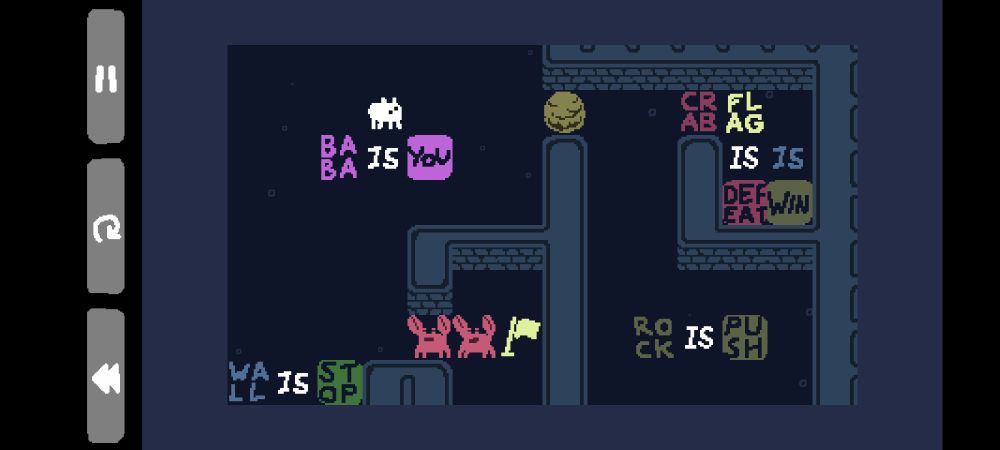
Projects like this are tough to pull off, and need users to play through the levels and find and eliminate things which the formalization is making artificially hard. Fork the repo and give the exercises a try!
Projects like this are tough to pull off, and need users to play through the levels and find and eliminate things which the formalization is making artificially hard. Fork the repo and give the exercises a try!
markushimmel.de/blog/my-firs...
markushimmel.de/blog/my-firs...




