Alex Squires
@agsquires.bsky.social
110 followers
74 following
4 posts
Group Leader in the Scanlon Materials Theory Group at UoB chemistry
Posts
Media
Videos
Starter Packs
Reposted by Alex Squires
Seán Kavanagh
@kavanaghsean.bsky.social
· Apr 15
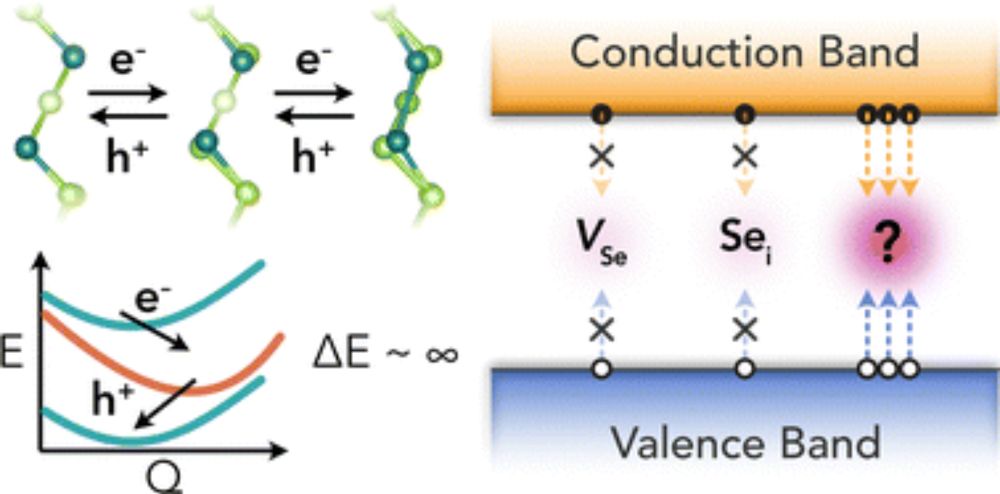
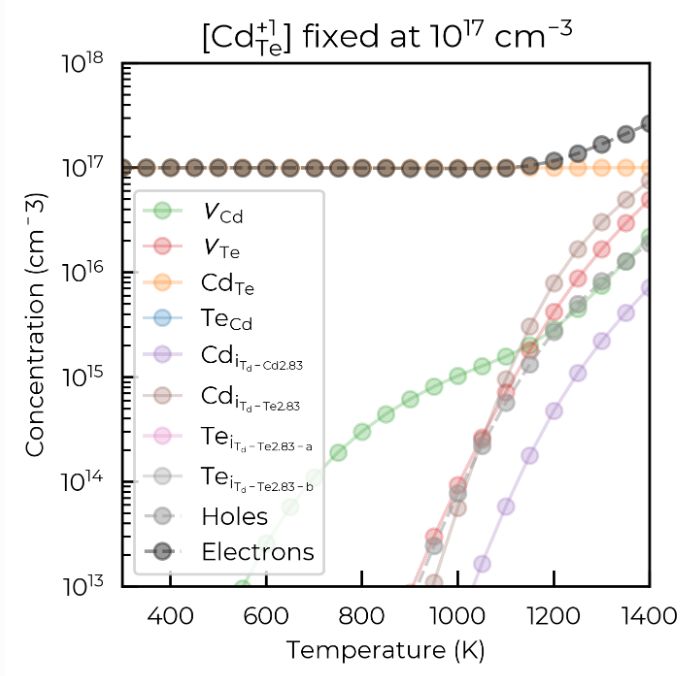
Intrinsic point defect tolerance in selenium for indoor and tandem photovoltaics
Selenium has reemerged as a promising absorber material for tandem and indoor photovoltaic (PV) devices due to its elemental simplicity, unique structural features, and wide band gap. However, despite...
pubs.rsc.org
Alex Squires
@agsquires.bsky.social
· Mar 13
Reposted by Alex Squires
Reposted by Alex Squires
An(drew) McC
@arm61.bsky.social
· Jan 27

On the Estimation of Centre of Mass in Periodic Systems
Calculation of the centre of mass of a group of particles in a periodically-repeating cell is an important aspect of chemical and physical simulation. One popular approach, described by Bai and Breen,...
arxiv.org
Reposted by Alex Squires
An(drew) McC
@arm61.bsky.social
· Dec 30

Accurate Estimation of Diffusion Coefficients and their Uncertainties from Computer Simulation
Self-diffusion coefficients, D*, are routinely estimated from molecular dynamics simulations by fitting a linear model to the observed mean squared displacements (MSDs) of mobile species. MSDs derived from simulations exhibit statistical noise that causes uncertainty in the resulting estimate of D*. An optimal scheme for estimating D* minimizes this uncertainty, i.e., it will have high statistical efficiency, and also gives an accurate estimate of the uncertainty itself. We present a scheme for estimating D* from a single simulation trajectory with a high statistical efficiency and accurately estimating the uncertainty in the predicted value. The statistical distribution of MSDs observable from a given simulation is modeled as a multivariate normal distribution using an analytical covariance matrix for an equivalent system of freely diffusing particles, which we parametrize from the available simulation data. We use Bayesian regression to sample the distribution of linear models that are compatible with this multivariate normal distribution to obtain a statistically efficient estimate of D* and an accurate estimate of the associated statistical uncertainty.
doi.org