Caleb Shor
@cshor.org
* Math professor at WNEU
* Director of PROMYS for Teachers at Boston University
* Travel enthusiast
* Fan of lists
* Director of PROMYS for Teachers at Boston University
* Travel enthusiast
* Fan of lists
Gracias.
I’m toying with the idea a problem set about dissecting squares into triangles for the next workshop. Thoughts? I can hold off, esp if you could attend somehow (in person or zoom) next semester.
I’m toying with the idea a problem set about dissecting squares into triangles for the next workshop. Thoughts? I can hold off, esp if you could attend somehow (in person or zoom) next semester.
October 19, 2025 at 11:07 PM
Gracias.
I’m toying with the idea a problem set about dissecting squares into triangles for the next workshop. Thoughts? I can hold off, esp if you could attend somehow (in person or zoom) next semester.
I’m toying with the idea a problem set about dissecting squares into triangles for the next workshop. Thoughts? I can hold off, esp if you could attend somehow (in person or zoom) next semester.
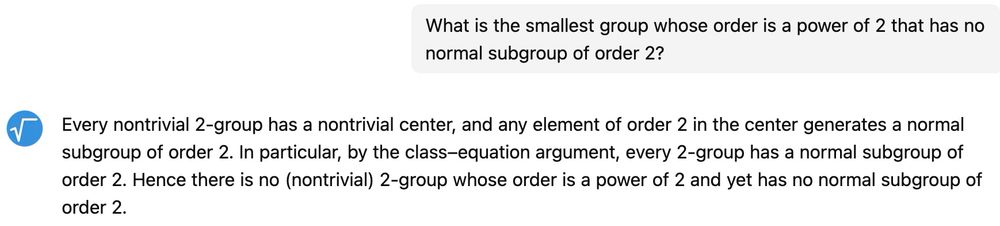
FWIW, I just typed this prompt into math-gpt.org and it answered the question correctly.
(There appear to be a few math gpt websites. That’s the first one that appeared when I searched.)
(There appear to be a few math gpt websites. That’s the first one that appeared when I searched.)
May 25, 2025 at 7:06 PM
FWIW, I just typed this prompt into math-gpt.org and it answered the question correctly.
(There appear to be a few math gpt websites. That’s the first one that appeared when I searched.)
(There appear to be a few math gpt websites. That’s the first one that appeared when I searched.)
Looks to me like you negated both the numerator and denominator (instead of just one of them) in the very last step. Otherwise I buy it.
May 19, 2025 at 9:36 PM
Looks to me like you negated both the numerator and denominator (instead of just one of them) in the very last step. Otherwise I buy it.
Thank you for sharing tonight! And on such short notice. Always great to see you. I like the way your brain works.
March 13, 2025 at 2:29 AM
Thank you for sharing tonight! And on such short notice. Always great to see you. I like the way your brain works.
I like this approach! As I read it I was going to mention that it’s in the pcmi materials. And then I finished reading what you wrote. Ha!
March 13, 2025 at 2:26 AM
I like this approach! As I read it I was going to mention that it’s in the pcmi materials. And then I finished reading what you wrote. Ha!
Hadn’t seen that! Thank you for sharing it. You have some really great MO posts.
March 1, 2025 at 2:55 AM
Hadn’t seen that! Thank you for sharing it. You have some really great MO posts.
The problem is quite doable without any knowledge of Legendre symbols btw.
and sending you stuff is on my to do list.
and sending you stuff is on my to do list.
February 28, 2025 at 9:58 PM
The problem is quite doable without any knowledge of Legendre symbols btw.
and sending you stuff is on my to do list.
and sending you stuff is on my to do list.
Ha. That was a fun read. There’s actually a lot of good stuff in there. A lot of handwaving too — not sure it’s providing a ton of insight. The key is why that sum of (n/p) * ((n+1)/p) is -1, which it dodges explaining. I’m not sure that’s a “well-known result” as is claimed.
February 28, 2025 at 7:16 PM
Ha. That was a fun read. There’s actually a lot of good stuff in there. A lot of handwaving too — not sure it’s providing a ton of insight. The key is why that sum of (n/p) * ((n+1)/p) is -1, which it dodges explaining. I’m not sure that’s a “well-known result” as is claimed.
Err, squares mod p. Blah.
February 26, 2025 at 4:02 AM
Err, squares mod p. Blah.
I like the quiz very much.
And I will share materials. Seriously. Previously I had the excuse that I was traveling. Now I’m not. But my computer is waaaay over there.
Here’s a problem I saw recently. For p prime, how many integers n in {0,1,…,p-1} have the property that n and n+1 are both squares?
And I will share materials. Seriously. Previously I had the excuse that I was traveling. Now I’m not. But my computer is waaaay over there.
Here’s a problem I saw recently. For p prime, how many integers n in {0,1,…,p-1} have the property that n and n+1 are both squares?
February 26, 2025 at 3:41 AM
I like the quiz very much.
And I will share materials. Seriously. Previously I had the excuse that I was traveling. Now I’m not. But my computer is waaaay over there.
Here’s a problem I saw recently. For p prime, how many integers n in {0,1,…,p-1} have the property that n and n+1 are both squares?
And I will share materials. Seriously. Previously I had the excuse that I was traveling. Now I’m not. But my computer is waaaay over there.
Here’s a problem I saw recently. For p prime, how many integers n in {0,1,…,p-1} have the property that n and n+1 are both squares?
I really like that fact about n dividing a number that’s all 9s! It’s a good one. I often put that on the final exam when I teach number theory.
February 26, 2025 at 3:32 AM
I really like that fact about n dividing a number that’s all 9s! It’s a good one. I often put that on the final exam when I teach number theory.
Pretty sure! Otherwise the whole state would be shut down and we’d be open. (Kind of like on Presidents’ Day.)
February 18, 2025 at 2:29 PM
Pretty sure! Otherwise the whole state would be shut down and we’d be open. (Kind of like on Presidents’ Day.)
That seems reasonable. Are your students using it as well?
February 15, 2025 at 5:45 AM
That seems reasonable. Are your students using it as well?
I haven’t seen any compelling reason to like it for the math I teach or do.
The main thing I’ve seen is students using it to pass off its “work” as their own. Maybe it’s good for certain subjects, but eg AI-produced proofs in an abstract algebra course are hot garbage.
The main thing I’ve seen is students using it to pass off its “work” as their own. Maybe it’s good for certain subjects, but eg AI-produced proofs in an abstract algebra course are hot garbage.
February 15, 2025 at 1:32 AM
I haven’t seen any compelling reason to like it for the math I teach or do.
The main thing I’ve seen is students using it to pass off its “work” as their own. Maybe it’s good for certain subjects, but eg AI-produced proofs in an abstract algebra course are hot garbage.
The main thing I’ve seen is students using it to pass off its “work” as their own. Maybe it’s good for certain subjects, but eg AI-produced proofs in an abstract algebra course are hot garbage.
I see a second player win. Player 2 (P2) selects the same 4 rows as player 1 (P1). Call those rows A, B, C, D.
If P1 makes a move in one of rows A and B, P2 makes the same move in the other row. Same idea for rows C and D.
This way, whenever P1 has a valid move, P2 does too. Fun!
If P1 makes a move in one of rows A and B, P2 makes the same move in the other row. Same idea for rows C and D.
This way, whenever P1 has a valid move, P2 does too. Fun!
February 11, 2025 at 5:28 PM
I see a second player win. Player 2 (P2) selects the same 4 rows as player 1 (P1). Call those rows A, B, C, D.
If P1 makes a move in one of rows A and B, P2 makes the same move in the other row. Same idea for rows C and D.
This way, whenever P1 has a valid move, P2 does too. Fun!
If P1 makes a move in one of rows A and B, P2 makes the same move in the other row. Same idea for rows C and D.
This way, whenever P1 has a valid move, P2 does too. Fun!
This was fun. The extra helpful part at the end made me laugh!
February 2, 2025 at 10:16 PM
This was fun. The extra helpful part at the end made me laugh!