Posts
Media
Videos
Starter Packs
Reposted by David Beers
Reposted by David Beers
Reposted by David Beers
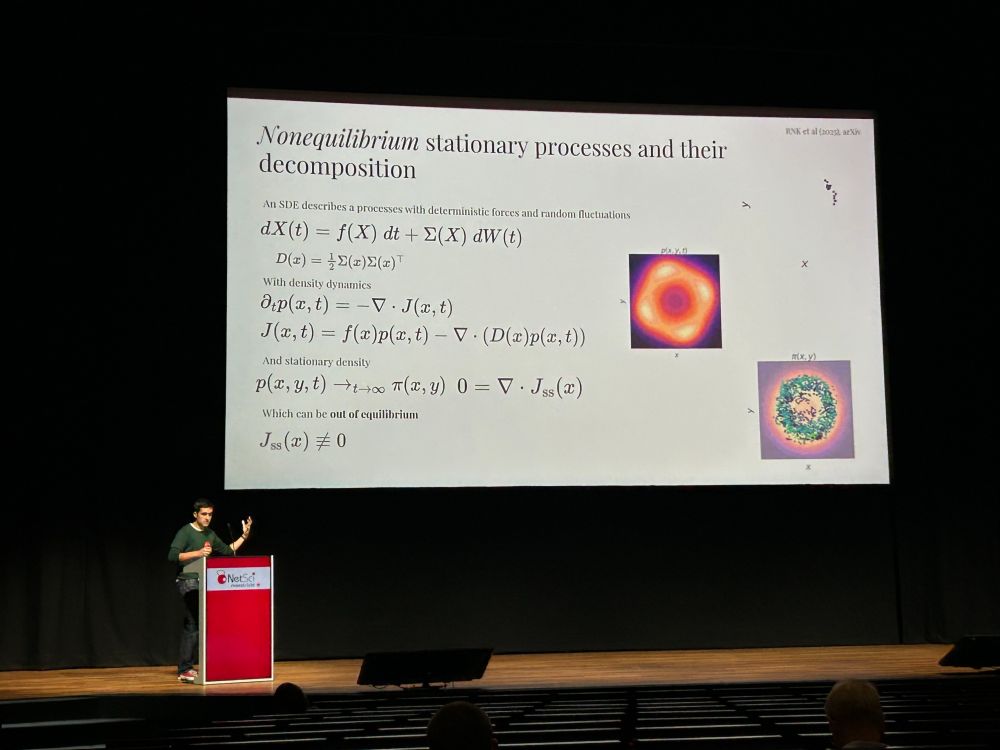
David Beers
@davidbeersmath.bsky.social
· May 27
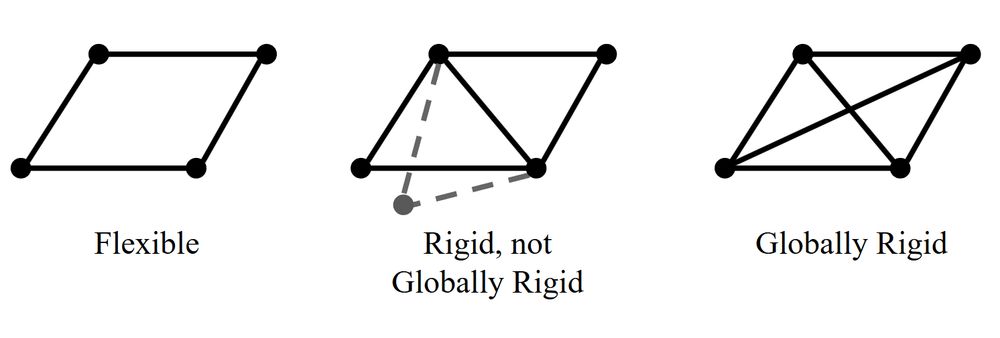
David Beers
@davidbeersmath.bsky.social
· May 27
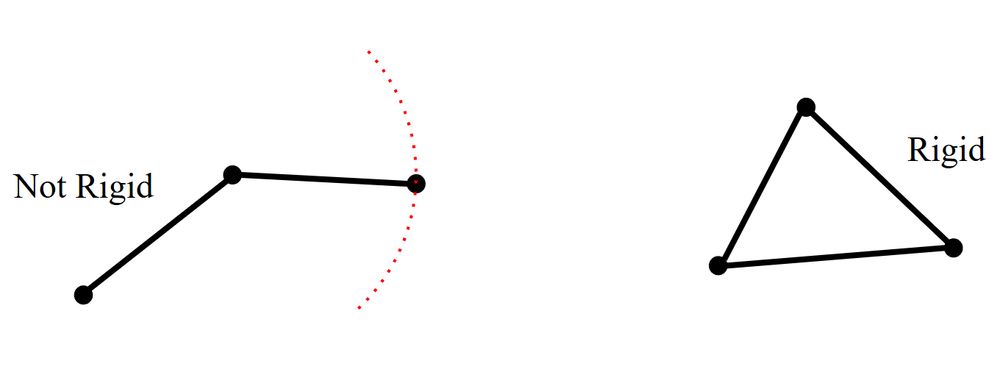
David Beers
@davidbeersmath.bsky.social
· May 27
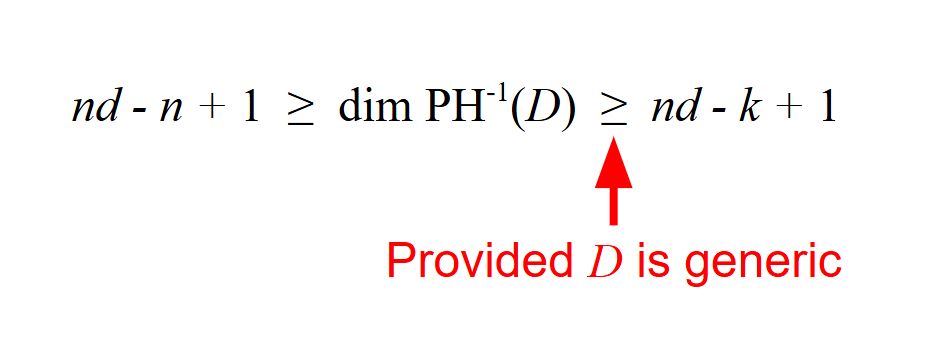
David Beers
@davidbeersmath.bsky.social
· May 27
David Beers
@davidbeersmath.bsky.social
· May 27