
www.threads.com/@florisium.g...
www.threads.com/@florisium.g...
And finally, here are a few fresh in-game shots (and remember - the game is still about flowers! 🌸)
(16/16)




And finally, here are a few fresh in-game shots (and remember - the game is still about flowers! 🌸)
(16/16)
(15/16)


(15/16)
On an iPhone 15Pro, native res, it costs about 0.02–0.2ms, depending on scene complexity and density (all are combined to a single draw-call).
(14/16)
On an iPhone 15Pro, native res, it costs about 0.02–0.2ms, depending on scene complexity and density (all are combined to a single draw-call).
(14/16)
The result is much more detailed and believable than the old texture-based version.
Left = old. Right = new.
(13/16)


The result is much more detailed and believable than the old texture-based version.
Left = old. Right = new.
(13/16)
(12/16)


(12/16)
I ended up with a slightly different, yet still cheap, function that models the visibility per rectangle size - same logic as with cylinders.
(11/16)


I ended up with a slightly different, yet still cheap, function that models the visibility per rectangle size - same logic as with cylinders.
(11/16)
This separation (vertical+horizontal) produces results that are visually close to ray-traced truth - see the right image (distances and heights are not correlated on the images):
(10/16)


This separation (vertical+horizontal) produces results that are visually close to ray-traced truth - see the right image (distances and heights are not correlated on the images):
(10/16)
The horizontal part, though, depends on how visibility changes with the distance to the surface and the surface’s own size.
The horizontal part, though, depends on how visibility changes with the distance to the surface and the surface’s own size.
Ideally, this should be a hemispherical integral of point visibility.
In practice, I simplified it by splitting it into vertical and horizontal 2D components.
(9/16)
Ideally, this should be a hemispherical integral of point visibility.
In practice, I simplified it by splitting it into vertical and horizontal 2D components.
(9/16)
That gives a lightweight, computation-friendly formula that still behaves like smooth, realistic occlusion.
You can play with the simplified version here: www.desmos.com/calculator/j...
(8/16)
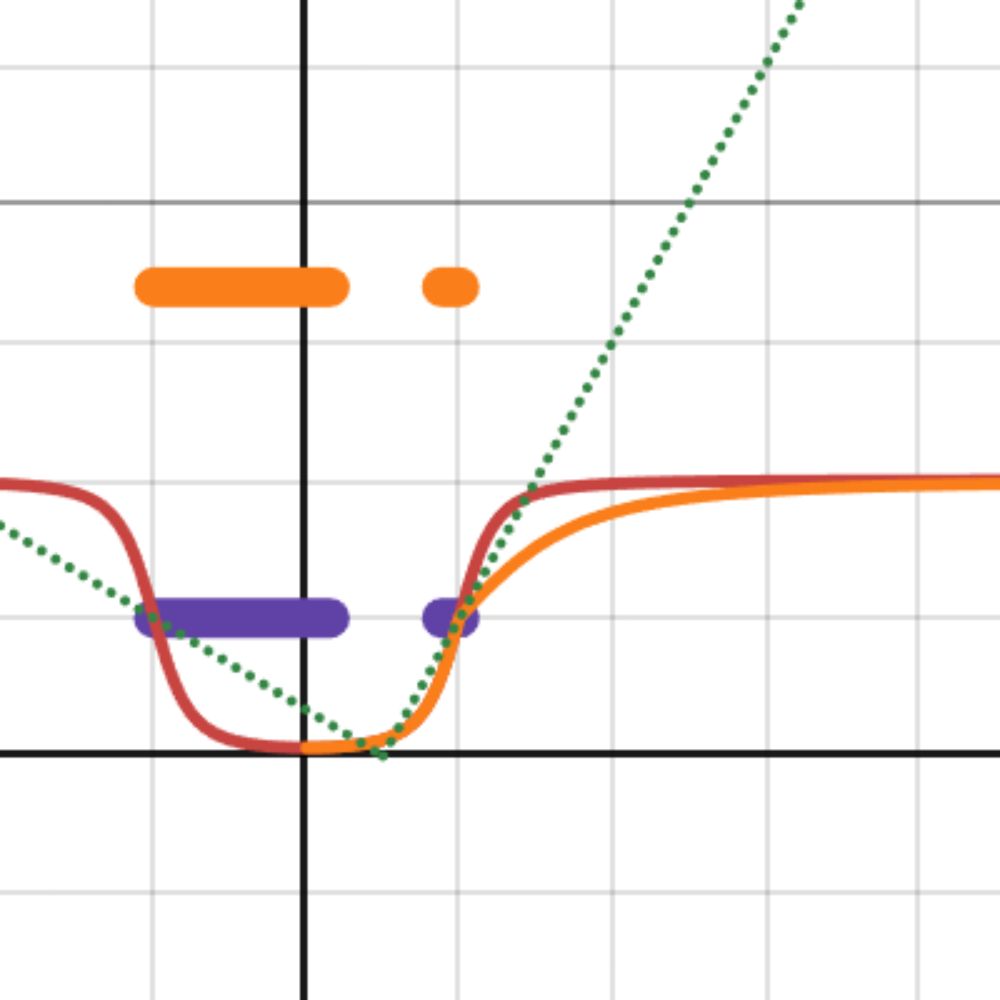
That gives a lightweight, computation-friendly formula that still behaves like smooth, realistic occlusion.
You can play with the simplified version here: www.desmos.com/calculator/j...
(8/16)
Imagine a flat occluder of width 2W(from -W to W) standing at height H.
The occlusion function looks like:
(cos(arctan((x - W)/H)) + cos(arctan((-x - W)/H))) / 2 + 1
In other words - the sum of light coming from the left and right gaps around the occluder.
(7/16)

Imagine a flat occluder of width 2W(from -W to W) standing at height H.
The occlusion function looks like:
(cos(arctan((x - W)/H)) + cos(arctan((-x - W)/H))) / 2 + 1
In other words - the sum of light coming from the left and right gaps around the occluder.
(7/16)
This time - no prebaked textures.
Instead, I went analytical - doing the math to emulate occlusion shapes directly for some simple primitives (boxes, spheres, cylinders, cones, etc).
(6/16)
This time - no prebaked textures.
Instead, I went analytical - doing the math to emulate occlusion shapes directly for some simple primitives (boxes, spheres, cylinders, cones, etc).
(6/16)
But... it was never perfect. Fixed textures have obvious limits.
(5/16)
But... it was never perfect. Fixed textures have obvious limits.
(5/16)
Just 3 texture types - pulled on for every moving object in the game (could be more than 1 shape per object).
It worked!

Just 3 texture types - pulled on for every moving object in the game (could be more than 1 shape per object).
It worked!
5. And yeah - do the above for every occlusion-receiver pair 😅
(4/16)

5. And yeah - do the above for every occlusion-receiver pair 😅
(4/16)
1. Define surfaces that receive occlusion.
2. Define objects that cast occlusion.
3. For each receiver–caster pair, compute the projected occlusion area that roughly estimates shadowing of the cast object.
1. Define surfaces that receive occlusion.
2. Define objects that cast occlusion.
3. For each receiver–caster pair, compute the projected occlusion area that roughly estimates shadowing of the cast object.
(3/16)

(3/16)
Screen-space AO? Not great for mobile-too noisy, not tile-based GPU friendly, inconsistent across devices, and needs heavy filtering.
Ray-traced AO? Same story-not (yet?) practical on mobile.
(2/16)
Screen-space AO? Not great for mobile-too noisy, not tile-based GPU friendly, inconsistent across devices, and needs heavy filtering.
Ray-traced AO? Same story-not (yet?) practical on mobile.
(2/16)

