Jer
@jermath.bsky.social
I'd like to say I did that, but I doubled the 27 three times. When I got 216 I realized that would have been easier.
November 10, 2025 at 4:53 PM
I'd like to say I did that, but I doubled the 27 three times. When I got 216 I realized that would have been easier.
Some "let them eat cake" energy going on there
October 31, 2025 at 6:39 PM
Some "let them eat cake" energy going on there
It's funny because it's true.
(Or the least untrue things he's posted.)
(Or the least untrue things he's posted.)
October 29, 2025 at 11:52 PM
It's funny because it's true.
(Or the least untrue things he's posted.)
(Or the least untrue things he's posted.)
I don't think your argument is sound. There's no guarantee that for any P the triangular cross-section can be adjusted by epsilon and intersect all six sides. On a cube-like shape it does, but for my shape it sometimes can't. Does every F=6, V=8 shape have some P that does work?
October 8, 2025 at 6:08 PM
I don't think your argument is sound. There's no guarantee that for any P the triangular cross-section can be adjusted by epsilon and intersect all six sides. On a cube-like shape it does, but for my shape it sometimes can't. Does every F=6, V=8 shape have some P that does work?
Looks like you can get a hexagon. At least for this simple case. www.desmos.com/3d/brrufqrvj4

Desmos | 3D Graphing Calculator
www.desmos.com
October 8, 2025 at 1:53 PM
Looks like you can get a hexagon. At least for this simple case. www.desmos.com/3d/brrufqrvj4
No. A tetrahedron with the tips of two corners sliced off fits the description. I'm having trouble picturing whether it has a hexagonal cross-section.
October 8, 2025 at 1:35 PM
No. A tetrahedron with the tips of two corners sliced off fits the description. I'm having trouble picturing whether it has a hexagonal cross-section.
You guessed correctly. I don't have that one, just the ones that skip by constant amounts.
September 18, 2025 at 3:46 PM
You guessed correctly. I don't have that one, just the ones that skip by constant amounts.
I think I've cracked it. For any even number of people, there are none (I think). For 7, there are 5. For 9, just 3. (I don't know if I'm missing some sporadic cases, though.)
September 17, 2025 at 7:12 PM
I think I've cracked it. For any even number of people, there are none (I think). For 7, there are 5. For 9, just 3. (I don't know if I'm missing some sporadic cases, though.)
Another arrangement is acebd, which is its own dual, matching in the same order: ACEBD.
September 15, 2025 at 4:18 PM
Another arrangement is acebd, which is its own dual, matching in the same order: ACEBD.
Call your arrangement aedbc, and it matches ADBEC after each rotation pictures. The alternate arrangement adbec matches AEDCB. Swap lower-case letters with upper.
September 15, 2025 at 3:36 PM
Call your arrangement aedbc, and it matches ADBEC after each rotation pictures. The alternate arrangement adbec matches AEDCB. Swap lower-case letters with upper.

Desmos | Graphing Calculator
www.desmos.com
September 13, 2025 at 8:06 PM
It seems like the area is not unique. If the triangle is zero the area is 90.25. If it takes up half the square, the isoceles right triangle has area 361(3-2sqrt2) = 61.94. I think there is a missing constraint based on the Pythagoras tag.
September 13, 2025 at 8:01 PM
It seems like the area is not unique. If the triangle is zero the area is 90.25. If it takes up half the square, the isoceles right triangle has area 361(3-2sqrt2) = 61.94. I think there is a missing constraint based on the Pythagoras tag.
The paper doesn't say every shape checked has the property, it only implies no counterexamples had been found. From the paper:
As of today, most of these polyhedra are known to have Rupert’s property, but some remain open.
As of today, most of these polyhedra are known to have Rupert’s property, but some remain open.
August 28, 2025 at 2:20 PM
The paper doesn't say every shape checked has the property, it only implies no counterexamples had been found. From the paper:
As of today, most of these polyhedra are known to have Rupert’s property, but some remain open.
As of today, most of these polyhedra are known to have Rupert’s property, but some remain open.
My damned backwards brain that still mixes up left and right: ∀ is an upside-down "A" bc it's the indefinite article that means there is one, or it exists. ∃ is a backwards E bc it means "for Every."
August 27, 2025 at 12:30 PM
My damned backwards brain that still mixes up left and right: ∀ is an upside-down "A" bc it's the indefinite article that means there is one, or it exists. ∃ is a backwards E bc it means "for Every."
Does $200 worth of groceries fill a whole bag, still?
August 5, 2025 at 4:50 PM
Does $200 worth of groceries fill a whole bag, still?
Spoiler in the graph. www.desmos.com/calculator/y...

Desmos | Graphing Calculator
www.desmos.com
August 3, 2025 at 1:20 AM
Spoiler in the graph. www.desmos.com/calculator/y...
Yes this one is easier. When a=sqrt(3)/3, Area=sqrt(3)/2 - 2/3 www.desmos.com/calculator/a...

Paddy 7/31/25
www.desmos.com
July 31, 2025 at 10:18 PM
Yes this one is easier. When a=sqrt(3)/3, Area=sqrt(3)/2 - 2/3 www.desmos.com/calculator/a...
Area when a=3 is 9/4 - sqrt(3) Not too bad. Work shown in Desmos. www.desmos.com/calculator/6...
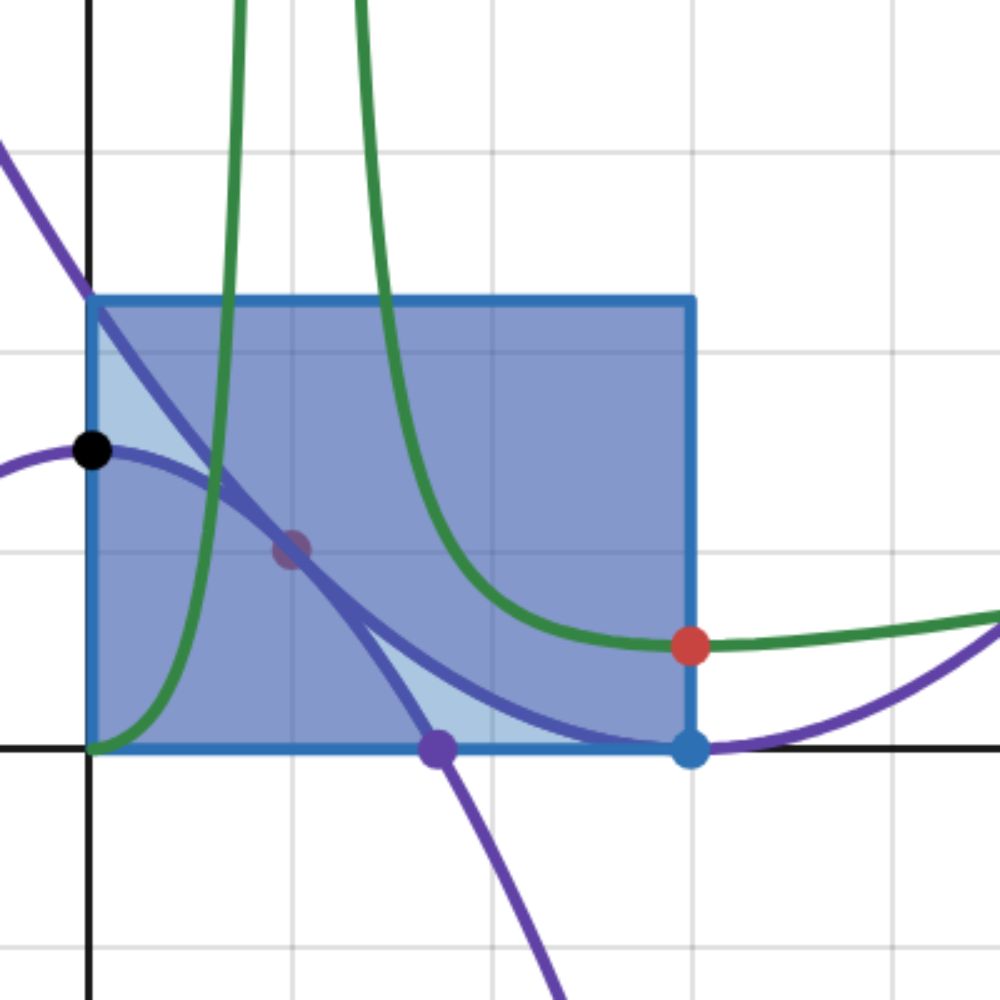
Paddy 7/30/25
www.desmos.com
July 31, 2025 at 9:46 PM
Area when a=3 is 9/4 - sqrt(3) Not too bad. Work shown in Desmos. www.desmos.com/calculator/6...
Those are the extremes, but A can be folded to anywhere along BC. The boundary is a smooth curve.
July 22, 2025 at 12:59 AM
Those are the extremes, but A can be folded to anywhere along BC. The boundary is a smooth curve.
Nice one. Here's a Desmos I whipped up. www.desmos.com/calculator/2...

Desmos | Graphing Calculator
www.desmos.com
July 22, 2025 at 12:58 AM
Nice one. Here's a Desmos I whipped up. www.desmos.com/calculator/2...
For completeness: the solutions. The first (black) has the nice rational crease of length 7.5, the second (orange) is a root of a degree 5 polynomial as found by WolframAlpha to be about 13.5907 I wonder if any perimeters have two rational solutions?
www.desmos.com/calculator/d...
www.desmos.com/calculator/d...

folded rectangle solutions
www.desmos.com
July 20, 2025 at 6:20 PM
For completeness: the solutions. The first (black) has the nice rational crease of length 7.5, the second (orange) is a root of a degree 5 polynomial as found by WolframAlpha to be about 13.5907 I wonder if any perimeters have two rational solutions?
www.desmos.com/calculator/d...
www.desmos.com/calculator/d...
Perimeter as a function of x, color coded as in the first graph. Time to start solving your question. y=39/11 hits both the black and orange portions.
www.desmos.com/calculator/5...
www.desmos.com/calculator/5...

ways to fold a rectangle perimeter formula
www.desmos.com
July 20, 2025 at 6:10 PM
Perimeter as a function of x, color coded as in the first graph. Time to start solving your question. y=39/11 hits both the black and orange portions.
www.desmos.com/calculator/5...
www.desmos.com/calculator/5...
My perimeter is 4 (can scale by 11 later) with sides AB=a and BC=2-a. You can see the crease will pass through different sides based on where a lies with respect to the interval [2/3, 4sqrt(3)-6] www.desmos.com/calculator/i...

Ways to fold a rectangle
www.desmos.com
July 20, 2025 at 6:03 PM
My perimeter is 4 (can scale by 11 later) with sides AB=a and BC=2-a. You can see the crease will pass through different sides based on where a lies with respect to the interval [2/3, 4sqrt(3)-6] www.desmos.com/calculator/i...
There are two solutions. If the rectangle is 6 by 16, the crease is 7.5. If the rectangle is 10.233 by 11.776 the crease is about 13.591. I will follow up with some Desmos graphs. There are three ways this crease can go.
July 20, 2025 at 5:52 PM
There are two solutions. If the rectangle is 6 by 16, the crease is 7.5. If the rectangle is 10.233 by 11.776 the crease is about 13.591. I will follow up with some Desmos graphs. There are three ways this crease can go.
This was the Pioneer Valley All Day Sing. The Western Mass Convention is two days in early March. (Also check out the Berkshire Foothills All Day in November.) Everything else checks out for sure.
July 12, 2025 at 10:17 PM
This was the Pioneer Valley All Day Sing. The Western Mass Convention is two days in early March. (Also check out the Berkshire Foothills All Day in November.) Everything else checks out for sure.

