When Dr. Average Scientist publishes a paper, nobody notices, nobody reads it without some leg work to get it out there
When Dr. Average Scientist publishes a paper, nobody notices, nobody reads it without some leg work to get it out there
Plasticity rules like Oja's let us go beyond studying how synaptic plasticity in the brain can _match_ the performance of backprop.
Now, we can study how synaptic plasticity can _beat_ backprop in challenging, but realistic learning scenarios.
Plasticity rules like Oja's let us go beyond studying how synaptic plasticity in the brain can _match_ the performance of backprop.
Now, we can study how synaptic plasticity can _beat_ backprop in challenging, but realistic learning scenarios.






One plasticity rule improved learning, but its weight updates weren't aligned with backprop's. It was doing something different. That rule is Oja's plasticity rule.

One plasticity rule improved learning, but its weight updates weren't aligned with backprop's. It was doing something different. That rule is Oja's plasticity rule.

I just think that unless we're talking just about anatomy and we're restricting to a direct synaptic pathway (which maybe you are) then it's difficult to make this type of question precise without concluding that everything can query everything
I just think that unless we're talking just about anatomy and we're restricting to a direct synaptic pathway (which maybe you are) then it's difficult to make this type of question precise without concluding that everything can query everything
1) large negative eigenvalues are not necessary for LRS, and
2) high-dim input and stable dynamics are not sufficient for high-dim responses.
Motivated by this conversation, I added eigenvalues to the plot and edited the text a bit, thx!
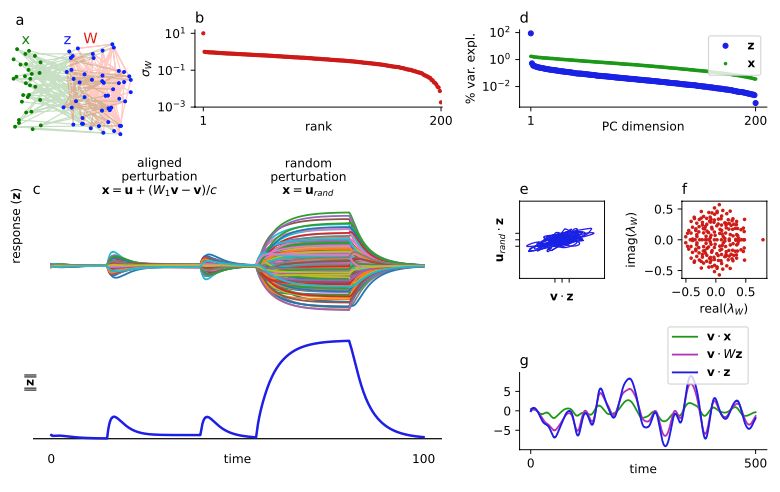
1) large negative eigenvalues are not necessary for LRS, and
2) high-dim input and stable dynamics are not sufficient for high-dim responses.
Motivated by this conversation, I added eigenvalues to the plot and edited the text a bit, thx!
How to derive the decay rate of the var expl vals in terms of the sing val decay rate and the overlap matrix?
How to derive the decay rate of the var expl vals in terms of the sing val decay rate and the overlap matrix?

