But on the sphere (like in Euclidean space) minimizers of the perimeter are just geodesic balls! So in this subcritical regime surface-tension wins and contracts Ω to a ball. In particular no interesting fine-scale patterns can appear.

More info here:
arxiv.org/abs/2601.10481

We find that there is a threshold for the interaction strength below which the energy becomes* a multiple of Per(Ω).

*In the sense of Γ-convergence.

Back to our initial motivation: non-local isoperimetric energies on the round sphere.

It turns out that the energy can be expressed in terms of the autocorrelation function, just like in the flat case. And this allows us to investigate the limit as the interaction range shrinks.

We show this function captures both, the volume and perimeter of Ω. More precisely, it is Lipschitz iff the set has finite perimeter, and its derivative at r=0 is proportional to Per(Ω).

This is a direct generalization of a result by Galerne in the Euclidean case.

Our insight: Replace translations with the geodesic flow.

Instead of sliding Ω around as a whole, let each point flow along all geodesics for a fixed distance r, then measure overlap.

This is our definition for a Riemannian version of the autocorrelation function.

But on a curved manifold, you can't "translate" a set—there's no global notion of moving things by a fixed vector. So how do we generalize?

Well, there is a local notion. We can certainly translate each point along all geodesics through it. That's what the geodesic flow does.

In flat space, a key tool is the autocorrelation function: it measures the average overlap between a set Ω and all its translates at distance r. It's closely related to Matheron's covariogram from stochastic geometry.

This has been investigated mainly for flat domains. For example, it is known that patterns only form if repulsion is strong enough.

But many patterns in biology occur on curved surfaces! So we wanted to see if curvature changes things and extend this to the round sphere.

Non-local isoperimetric energies model pattern formation on biological membranes. They balance perimeter minimization (think: cohesion/surface tension) with a long-range repulsive interaction (think: electrostatic repulsion between lipid head groups).

With 132 participants, it was the first event of this scale to unite the research communities across all three fields – building bridges and allowing for new collaboration between areas that have traditionally developed independently. (2/4)

⚡ A favorite among participants: the lightning sessions, offering early-career researchers a stage to share ideas and connect.

The event was organized by Anna Wienhard, Freya Jensen, Levin Maier, Diaaeldin Taha, and Michael Bleher. (4/4)

🤝 Jointly organized by Max-Planck-Institut für Mathematik in den Naturwissenschaften and STRUCTURES Cluster of Excellence Heidelberg, the workshop featured inspiring keynote talks, expert presentations, and contributions from industry partners like DeepMind, Deepshore, and Isomorphic Labs. (3/4)

Topology, causality, mechanistic interpretability, it's all in there.

open.substack.com/pub/subthaum...

Happy for any reactions, confused or otherwise.

Surely it's "A monad in X is just a monoid in the category of endofunctors of X, with product × replaced by composition of endofunctors and unit set by the identity endofunctor."

The second article:

Looks at adiabatic solutions of the Haydys-Witten equations and relates them to paths in the moduli space of EBE monopoles. This suggests a relation between Haydys-Witten instanton Floer homology and symplectic Khovanov homology.

https://arxiv.org/abs/2501.01365

The first article:

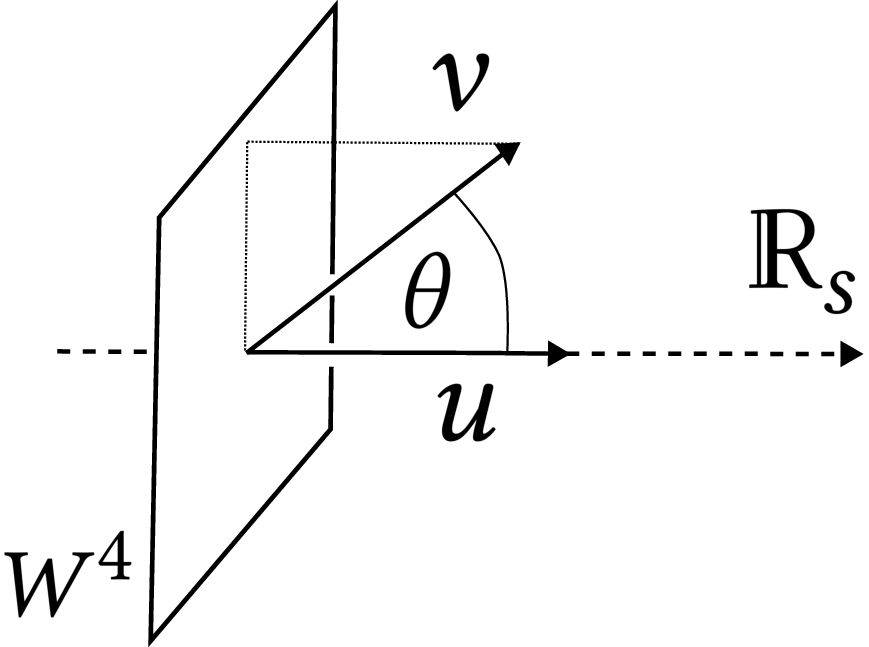
Introduces a one-parameter family of instanton Floer homology groups for four-manifolds, using the θ-Kapustin-Witten and Haydys-Witten equations. A conjecture by Witten links this to Khovanov homology for knots.

https://arxiv.org/abs/2412.13285

2/3