Lightnews — Scholar-powered news

William Gilpin @wgilpin.bsky.social · Jun 17

hi david, thank you very much :)

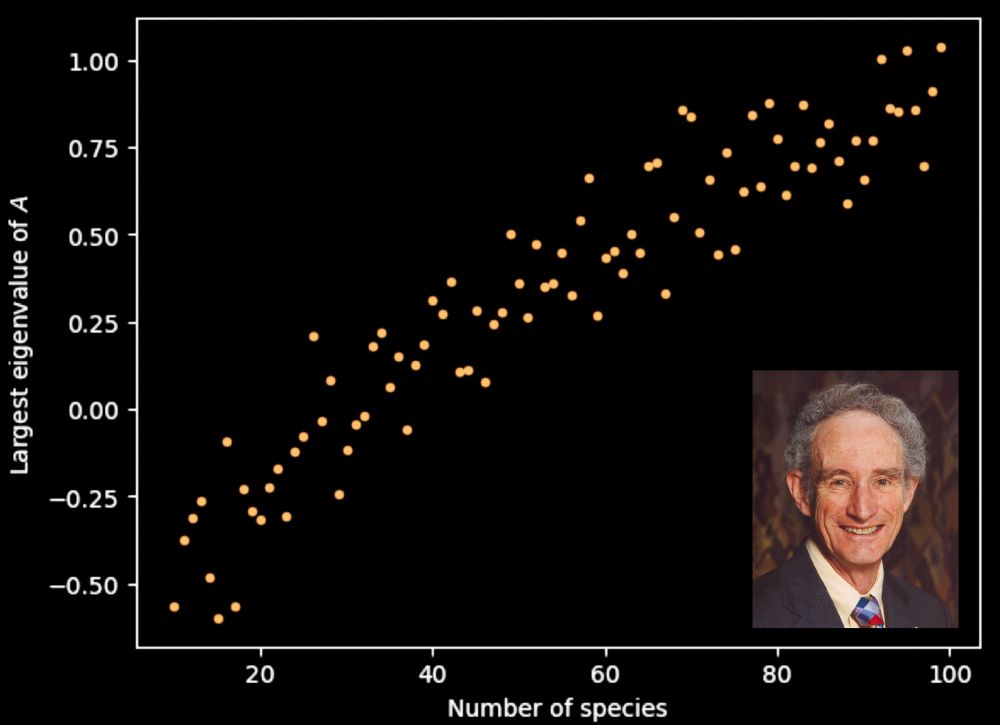
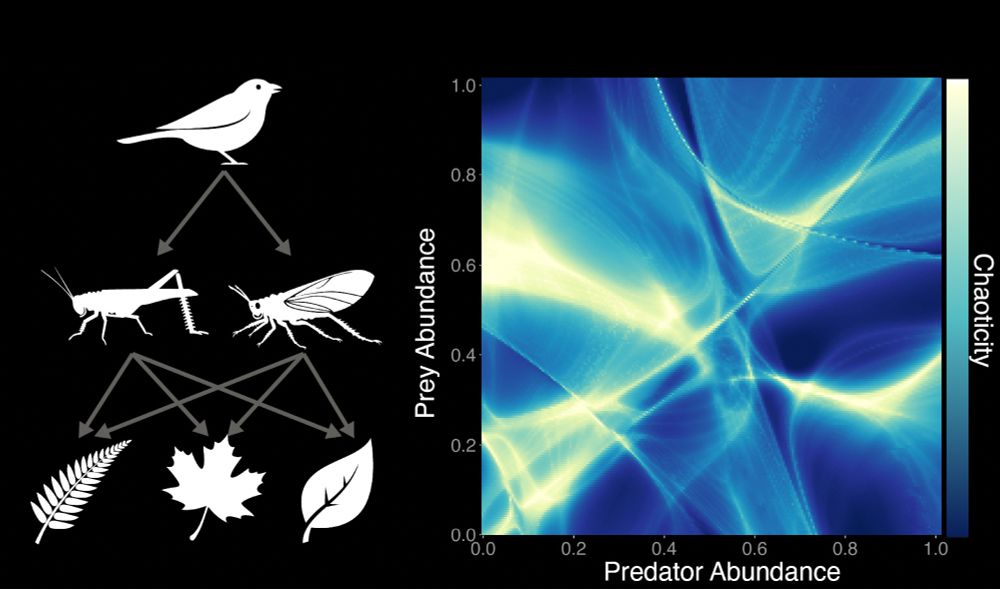
Optimization hardness constrains ecological transients

William Gilpin @wgilpin.bsky.social · Jun 16

Paper: doi.org/10.1371/jour...

Code: github.com/williamgilpi...

Explanatory Website & Code demo: williamgilpin.github.io/illotka/demo...

Author summary Distinct species can serve overlapping functions in complex ecosystems. For example, multiple cyanobacteria species within a microbial mat might serve to fix nitrogen. Here, we show mat...

doi.org

2

William Gilpin @wgilpin.bsky.social · Jun 16

This work was inspired by amazing recent work on transients by the dynamical systems community: Analogue KSAT solvers, slowdowns in gradient descent during neural network training, and chimera states in coupled oscillators. (12/N)

William Gilpin @wgilpin.bsky.social · Jun 16

For the Lotka-Volterra case, optimal coordinates are the right singular vectors of the species interaction matrix. You can experimentally estimate these with O(N) operations using Krylov-style methods: perturb the ecosystem, and see how it reacts. (11/N)

William Gilpin @wgilpin.bsky.social · Jun 16

This variation influences how we reduce the dimensionality of biological time series. With non-reciprocal interactions (like predator prey), PCA won’t always separate timescales. The optimal dimensionality-reducing variables (“ecomodes”) should precondition the linear problem (10/N)

William Gilpin @wgilpin.bsky.social · Jun 16

As a consequence of ill-conditioning, large ecosystems become excitable: small changes cause huge differences in how they approach equilibrium. Using the FLI, a metric invented by astrophysicists to study planetary orbits, we see caustics indicating variation in solve path (9/N)

William Gilpin @wgilpin.bsky.social · Jun 16

How would hard optimization problems arise in nature? I used genetic algorithms to evolve ecosystems towards supporting more biodiversity, and they became more ill-conditioned—and thus more prone to supertransients. (8/N)

William Gilpin @wgilpin.bsky.social · Jun 16

So ill-conditioning isn’t just something numerical analysts care about. It’s a physical property that measures computational complexity, which translates to super long equilibration times in large biological networks with trophic overlap (7/N)

William Gilpin @wgilpin.bsky.social · Jun 16

More precisely: the expected equilibration time of a random Lotka-Volterra system scales with the condition number of the species interaction matrix. The scaling matches the expected scaling of the solvers that your computer uses to do linear regression (6/N)

William Gilpin @wgilpin.bsky.social · Jun 16

We can think of ecological dynamics as an analogue constraint satisfaction problem. As the problem becomes more ill-conditioned, the ODEs describing the system take longer to “solve” the problem of who survives and who goes extinct (5/N)

William Gilpin @wgilpin.bsky.social · Jun 16

But is equilibrium even relevant? In high dimensions, stable fixed points might not be reachable in finite time. Supertransients due to unstable solutions that trap dynamics for increasingly long durations. E.g, pipe turbulence is supertransient (laminar flow is globally stable) (4/N)

William Gilpin @wgilpin.bsky.social · Jun 16

Dynamical systems are linear near fixed points, so May used random matrix theory to show large random ecosystems are usually unstable. The biodiversity we see in the real world requires finer-tuned structure from selection, niches, et al. that recover stability (3/N)

William Gilpin @wgilpin.bsky.social · Jun 16

A celebrated result in mathematical biology is Robert May’s “stability vs complexity” tradeoff. In large biological networks, we can’t possibly measure all N^2 interactions among N species, genes, neurons, etc. What is our null hypothesis for their behavior? (2/N)

GitHub - abao1999/panda: Patched Attention for Nonlinear Dynamics

William Gilpin @wgilpin.bsky.social · Jun 16

Does stability matter in biology? My article on the cover of this month’s @PLOSCompBiol explores how large ecosystems develop supertransients, a manifestation of computational hardness (1/N)

doi.org/10.1371/jour...

1 3 21

William Gilpin @wgilpin.bsky.social · May 22

Code here: github.com/abao1999/panda

Paper here: arxiv.org/abs/2505.13755

Study lead by Jeff Lai and Anthony Bao

Patched Attention for Nonlinear Dynamics. Contribute to abao1999/panda development by creating an account on GitHub.

github.com

2

William Gilpin @wgilpin.bsky.social · May 22

The attention architecture allows the model to handle much higher-dimensional inputs at testing than it ever saw during training, so we asked it to forecast two chaotic PDE (a fluid flow and KS equation). Not bad, given that the model has never seen a PDE before (6/7)

William Gilpin @wgilpin.bsky.social · May 22

We fed the model mixes of pure frequencies & measured its response. The activations lit up in complex patterns, indicating nonlinear resonance & mode-mixing, akin to triad interactions visible in turbulent bispectra. Compare these activations to Arnold webs in N-body chaos (5/7)

William Gilpin @wgilpin.bsky.social · May 22

We find a scaling law relating performance and the number of chaotic systems. Even if we control for total amount of training timepoints, more pretraining ODEs improves the model.

William Gilpin @wgilpin.bsky.social · May 22

What is the generalization signal for pretrained model to handle unseen chaotic systems? Post training, attention rollouts show recurrence maps and Toeplitz matrices, suggesting the model learns to implement complex numerical integration strategies to extend the context (5/8)

William Gilpin @wgilpin.bsky.social · May 22

Panda beats pure time-series foundation models at zero-shot forecasting unseen dynamical systems. That means that the model sees a snippet of an unseen chaotic system as context, and autonomously continues the dynamics (no weights are updated) (4/8)

William Gilpin @wgilpin.bsky.social · May 22

We made a novel chaotic systems dataset for pretaining by taking 135 hand-curated chaotic ODE (e.g. Lorenz, Rossler, etc) and mutating/recombining/selecting their ODE to select for chaoticity (3/8)

William Gilpin @wgilpin.bsky.social · May 22

Heroic effort co-lead by UT PhD students Jeff Lai & Anthony Bao, who implemented a new channel-attention architecture combining PatchTST, Takens embeddings, & Extended Dynamic Mode Decomp. They trained the whole thing on AMD GPUs! (2/8)