
Yuval Simons
@yuvalsim.bsky.social
Assistant professor at the University of Chicago. Studying the population genetics of complex traits (mainly) and interested in using math to understand biology.
Join my lab, where science is fun and traits are complex!
Join my lab, where science is fun and traits are complex!
It's a joke. Not a real quote
October 28, 2025 at 10:12 PM
It's a joke. Not a real quote
BTW, I'm always looking for students, postdocs, collaborators and minions. DM me if you're interested in working together.
October 24, 2025 at 2:18 AM
BTW, I'm always looking for students, postdocs, collaborators and minions. DM me if you're interested in working together.
(and apologies that the peer review process took so bloody long...)
October 24, 2025 at 1:53 AM
(and apologies that the peer review process took so bloody long...)
Endless thanks to @gcbias.bsky.social , @arbelharpak.bsky.social, @lukeoconnor.bsky.social, @docedge.bsky.social, @jgschraiber.bsky.social, @mollyprz.bsky.social, and the editors and (most) reviewers for providing indispensable feedback.
October 24, 2025 at 1:51 AM
Endless thanks to @gcbias.bsky.social , @arbelharpak.bsky.social, @lukeoconnor.bsky.social, @docedge.bsky.social, @jgschraiber.bsky.social, @mollyprz.bsky.social, and the editors and (most) reviewers for providing indispensable feedback.
This project could not have been done without the mentorship of @gs2747.bsky.social & @jkpritch.bsky.social and the hard work of @hakha.bsky.social , Julie Zhu and @courtsmithrun.bsky.social.
October 24, 2025 at 1:51 AM
This project could not have been done without the mentorship of @gs2747.bsky.social & @jkpritch.bsky.social and the hard work of @hakha.bsky.social , Julie Zhu and @courtsmithrun.bsky.social.
Side note: As part of the prolonged review process, we showed (in our supplement) using extensive data analysis and simulations that while COJO hits are not necessarily causal, they do a phenomenally good job at tagging the number, frequency and effect sizes of the true underlying causal variants.
October 24, 2025 at 1:51 AM
Side note: As part of the prolonged review process, we showed (in our supplement) using extensive data analysis and simulations that while COJO hits are not necessarily causal, they do a phenomenally good job at tagging the number, frequency and effect sizes of the true underlying causal variants.
Our conclusion is that the genetic architecture is well-described by a model of pleiotropic stabilizing selection, and well-approximated by a single distribution of selection coefficients for all traits. Differences between traits are driven by scaling with target size and heritability per site.
October 24, 2025 at 1:51 AM
Our conclusion is that the genetic architecture is well-described by a model of pleiotropic stabilizing selection, and well-approximated by a single distribution of selection coefficients for all traits. Differences between traits are driven by scaling with target size and heritability per site.
However, after we scale effect sizes by the heritability per site and account for differences in GWAS power, the genetic architectures of height and FEV1 look identical. The same is true for all other traits as well.

October 24, 2025 at 1:51 AM
However, after we scale effect sizes by the heritability per site and account for differences in GWAS power, the genetic architectures of height and FEV1 look identical. The same is true for all other traits as well.
The same isn’t true of traits that differ in their heritability per site, like height and FEV1.

October 24, 2025 at 1:51 AM
The same isn’t true of traits that differ in their heritability per site, like height and FEV1.
Therefore, two traits that differ in their target size but not in their heritability per site will differ only in the number of variants affecting them, but not in the variants’ joint distribution of frequencies and effect sizes. Just what we see for height and platelet crit.

October 24, 2025 at 1:51 AM
Therefore, two traits that differ in their target size but not in their heritability per site will differ only in the number of variants affecting them, but not in the variants’ joint distribution of frequencies and effect sizes. Just what we see for height and platelet crit.
The number of variants affecting a trait is proportional to the target size. The squared effect size of these variants (in units of the phenotypic variance) is proportional to the heritability per site, the heritability over the target size.
October 24, 2025 at 1:51 AM
The number of variants affecting a trait is proportional to the target size. The squared effect size of these variants (in units of the phenotypic variance) is proportional to the heritability per site, the heritability over the target size.
So why do traits differ in their genetic architecture?
While the distribution of selection coefficients is similar between traits, traits vastly differ in their target size and heritability.
The genetic architecture scales with these two parameters:
While the distribution of selection coefficients is similar between traits, traits vastly differ in their target size and heritability.
The genetic architecture scales with these two parameters:

October 24, 2025 at 1:51 AM
So why do traits differ in their genetic architecture?
While the distribution of selection coefficients is similar between traits, traits vastly differ in their target size and heritability.
The genetic architecture scales with these two parameters:
While the distribution of selection coefficients is similar between traits, traits vastly differ in their target size and heritability.
The genetic architecture scales with these two parameters:
As validation of our inferred distribution of selection coefficients we looked at allele ages:
RELATE infers the GWAS hits for our 95 traits to be younger than matched controls, indicating they are under selection. Our model predicts very well the distribution of allele ages.
RELATE infers the GWAS hits for our 95 traits to be younger than matched controls, indicating they are under selection. Our model predicts very well the distribution of allele ages.

October 24, 2025 at 1:51 AM
As validation of our inferred distribution of selection coefficients we looked at allele ages:
RELATE infers the GWAS hits for our 95 traits to be younger than matched controls, indicating they are under selection. Our model predicts very well the distribution of allele ages.
RELATE infers the GWAS hits for our 95 traits to be younger than matched controls, indicating they are under selection. Our model predicts very well the distribution of allele ages.
The single shared distribution (or SSD) model fits the data very well and much better than simple heuristic models with a Normal distribution of effect sizes.
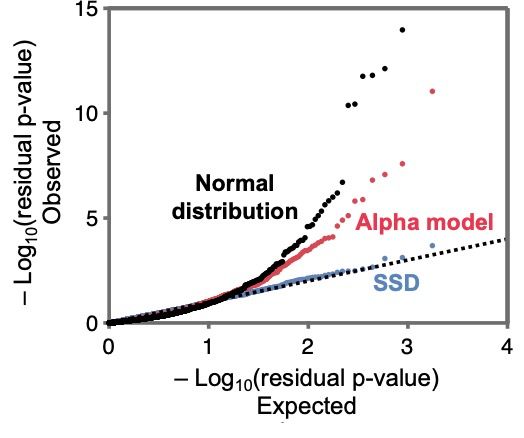
October 24, 2025 at 1:51 AM
The single shared distribution (or SSD) model fits the data very well and much better than simple heuristic models with a Normal distribution of effect sizes.
We therefore, suggest a useful approximation where we assume that there is a single shared distribution of selection coefficients among traits.

October 24, 2025 at 1:51 AM
We therefore, suggest a useful approximation where we assume that there is a single shared distribution of selection coefficients among traits.
We infer these 3 components for 95 continuous traits in the UK biobank.
While there are differences in the distribution of selection coefficients between traits, their confidence intervals overlap.
While there are differences in the distribution of selection coefficients between traits, their confidence intervals overlap.

October 24, 2025 at 1:51 AM
We infer these 3 components for 95 continuous traits in the UK biobank.
While there are differences in the distribution of selection coefficients between traits, their confidence intervals overlap.
While there are differences in the distribution of selection coefficients between traits, their confidence intervals overlap.
Our model has three components:
(1) The target size for a trait - the number of sites where a mutation would affect a given trait.
(2) The distribution of selection coefficients at those sites.
(3) The mean heritability per site – the heritability divided by the target size.
(1) The target size for a trait - the number of sites where a mutation would affect a given trait.
(2) The distribution of selection coefficients at those sites.
(3) The mean heritability per site – the heritability divided by the target size.

October 24, 2025 at 1:51 AM
Our model has three components:
(1) The target size for a trait - the number of sites where a mutation would affect a given trait.
(2) The distribution of selection coefficients at those sites.
(3) The mean heritability per site – the heritability divided by the target size.
(1) The target size for a trait - the number of sites where a mutation would affect a given trait.
(2) The distribution of selection coefficients at those sites.
(3) The mean heritability per site – the heritability divided by the target size.
We try to explain such differences by modeling how pleiotropic stabilizing selection shapes the genetic architecture of traits (building on our 2018 paper).
journals.plos.org/plosbiology/...
journals.plos.org/plosbiology/...

A population genetic interpretation of GWAS findings for human quantitative traits
Author summary One of the central goals of evolutionary genetics is to understand the processes that give rise to phenotypic variation in humans and other taxa. Genome-wide association studies (GWASs)...
journals.plos.org
October 24, 2025 at 1:51 AM
We try to explain such differences by modeling how pleiotropic stabilizing selection shapes the genetic architecture of traits (building on our 2018 paper).
journals.plos.org/plosbiology/...
journals.plos.org/plosbiology/...
For example, in the UK biobank, there are approximately 1500 independent GWAS hits for height which explain about 40% of height’s heritability. For FEV1, there are only 350 hits that explain roughly 10% of the heritability.
How can we explain such differences?
How can we explain such differences?
October 24, 2025 at 1:51 AM
For example, in the UK biobank, there are approximately 1500 independent GWAS hits for height which explain about 40% of height’s heritability. For FEV1, there are only 350 hits that explain roughly 10% of the heritability.
How can we explain such differences?
How can we explain such differences?
Even using the same dataset, GWAS for different traits identify different number of significantly-associated genetic variants (“GWAS hits”) for different traits and these variants explain different proportions of the traits’ heritabilities.
October 24, 2025 at 1:51 AM
Even using the same dataset, GWAS for different traits identify different number of significantly-associated genetic variants (“GWAS hits”) for different traits and these variants explain different proportions of the traits’ heritabilities.
Endless thanks to @gcbias.bsky.social, @arbelharpak.bsky.social, @lukeoconnor.bsky.social , @docedge.bsky.social, @jgschraiber.bsky.social , @mollyprz.bsky.social, and the editors and (most) reviewers for providing indispensable feedback.
October 24, 2025 at 1:40 AM
Endless thanks to @gcbias.bsky.social, @arbelharpak.bsky.social, @lukeoconnor.bsky.social , @docedge.bsky.social, @jgschraiber.bsky.social , @mollyprz.bsky.social, and the editors and (most) reviewers for providing indispensable feedback.
This project could not have been done without the mentorship of @gs2747.bsky.social & @jkpritch.bsky.social and the hard work of @hakha.bsky.social, Julie Zhu and @courtsmithrun.bsky.social.
October 24, 2025 at 1:40 AM
This project could not have been done without the mentorship of @gs2747.bsky.social & @jkpritch.bsky.social and the hard work of @hakha.bsky.social, Julie Zhu and @courtsmithrun.bsky.social.
Side note: As part of the prolonged review process, we showed (in our supplement) using extensive data analysis and simulations that while COJO hits are not necessarily causal, they do a phenomenally good job at tagging the number, frequency and effect sizes of the true underlying causal variants.
October 24, 2025 at 1:40 AM
Side note: As part of the prolonged review process, we showed (in our supplement) using extensive data analysis and simulations that while COJO hits are not necessarily causal, they do a phenomenally good job at tagging the number, frequency and effect sizes of the true underlying causal variants.

