
Many thanks to Charles Riou who already posted many videos of interviews of ML & stats researchers on his YouTube channel "ML New Papers"!! 🙏
Many thanks to Charles Riou who already posted many videos of interviews of ML & stats researchers on his YouTube channel "ML New Papers"!! 🙏
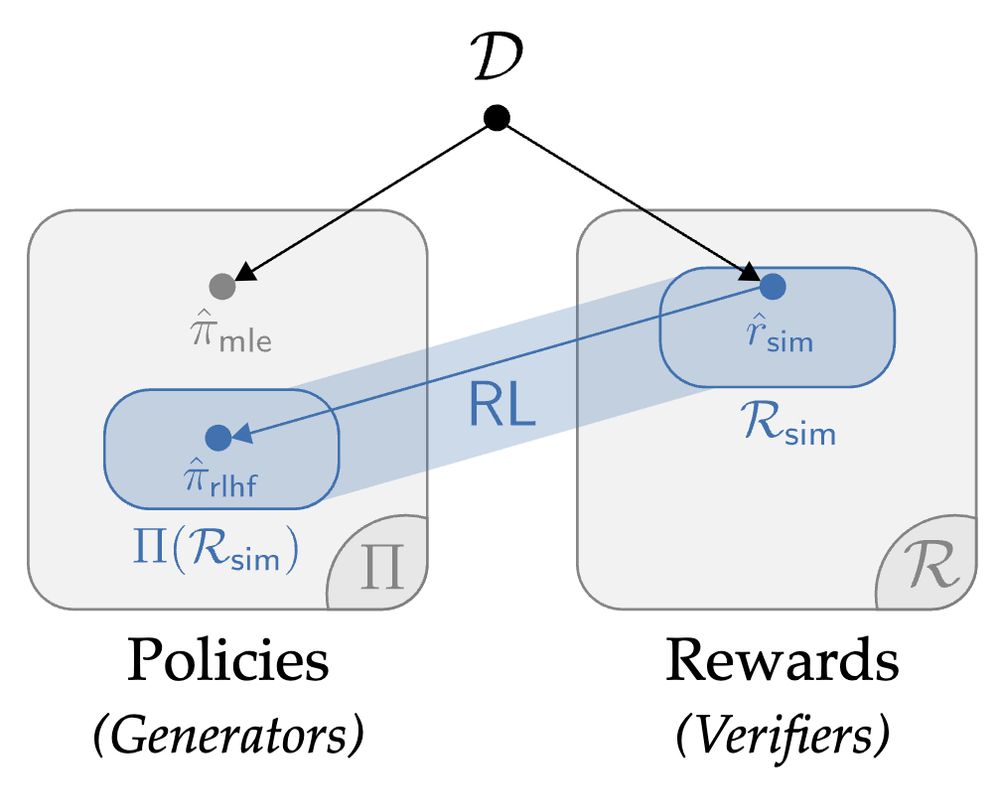
arxiv.org/abs/2502.04889




arxiv.org/abs/2502.04889
1) Joint Learning of Energy-based Models and their Partition Function
arxiv.org/abs/2501.18528
2) Loss Functions and Operators Generated by f-Divergences
arxiv.org/abs/2501.18537
A thread.
1) Joint Learning of Energy-based Models and their Partition Function
arxiv.org/abs/2501.18528
2) Loss Functions and Operators Generated by f-Divergences
arxiv.org/abs/2501.18537
A thread.
1) Joint Learning of Energy-based Models and their Partition Function
arxiv.org/abs/2501.18528
2) Loss Functions and Operators Generated by f-Divergences
arxiv.org/abs/2501.18537
A thread.
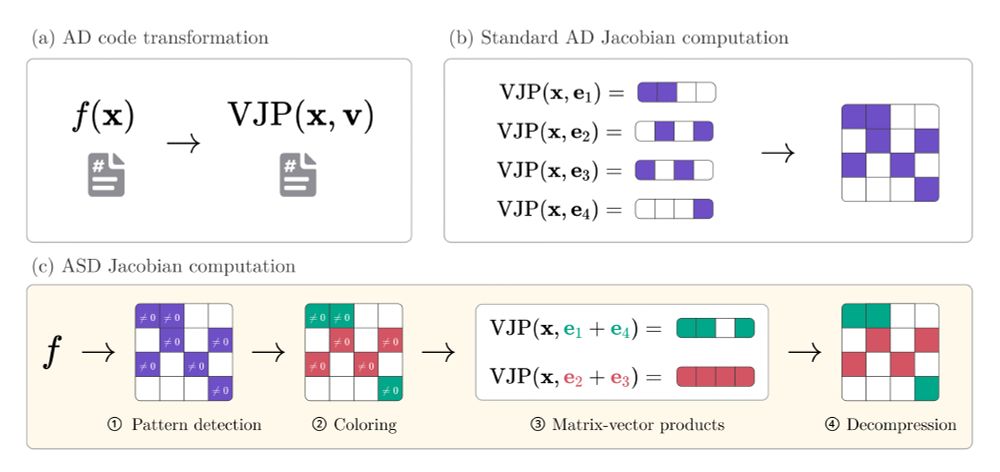
arxiv.org/abs/2501.17737
🧵1/8
probnum25.github.io

probnum25.github.io
📍 AIMS Mbour, Senegal
📅 June 23 - July 4, 2025
An international summer school to explore, collaborate, and deepen your understanding of machine learning in a unique and welcoming environment.
Details: mlss-senegal.github.io
📍 AIMS Mbour, Senegal
📅 June 23 - July 4, 2025
An international summer school to explore, collaborate, and deepen your understanding of machine learning in a unique and welcoming environment.
Details: mlss-senegal.github.io
📑 100 papers from NeurIPS 2024. Nearly twice as many as in 2023!
🧑🎓 over 300 registered participants
✅ a local and sustainable alternative to flying to Vancouver.
More info: neuripsinparis.github.io/neurips2024p...
📑 100 papers from NeurIPS 2024. Nearly twice as many as in 2023!
🧑🎓 over 300 registered participants
✅ a local and sustainable alternative to flying to Vancouver.
More info: neuripsinparis.github.io/neurips2024p...



