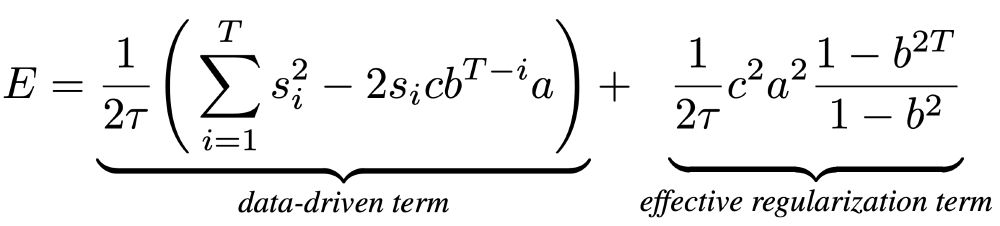Alexandra Proca
@aproca.bsky.social
96 followers
140 following
15 posts
PhD student at Imperial College London. theoretical neuroscience, machine learning. aproca.github.io
Posts
Media
Videos
Starter Packs
Alexandra Proca
@aproca.bsky.social
· Jun 20
Alexandra Proca
@aproca.bsky.social
· Jun 20
Alexandra Proca
@aproca.bsky.social
· Jun 20
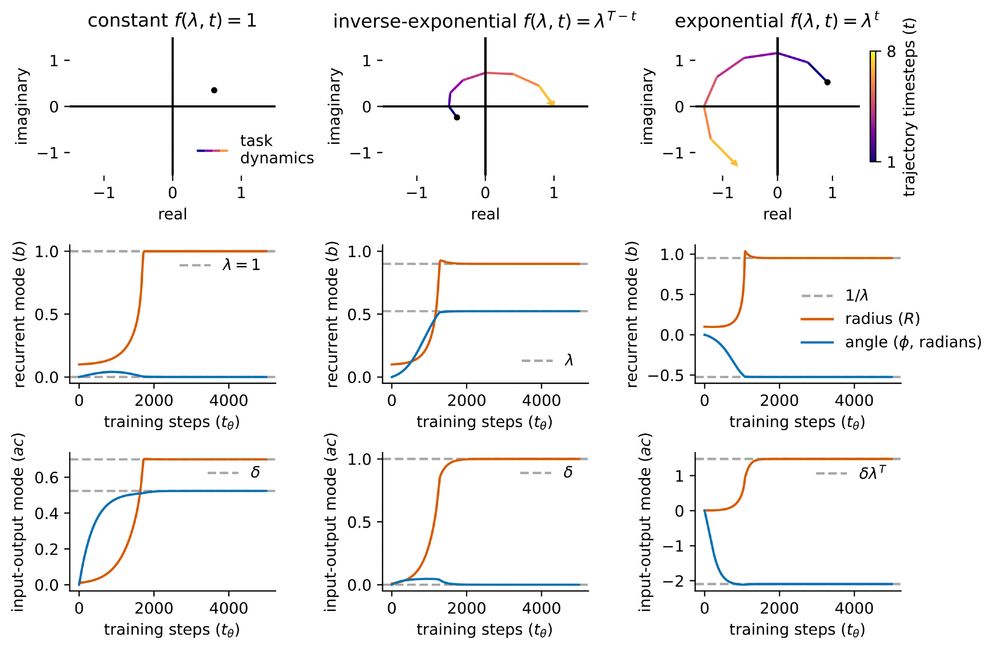
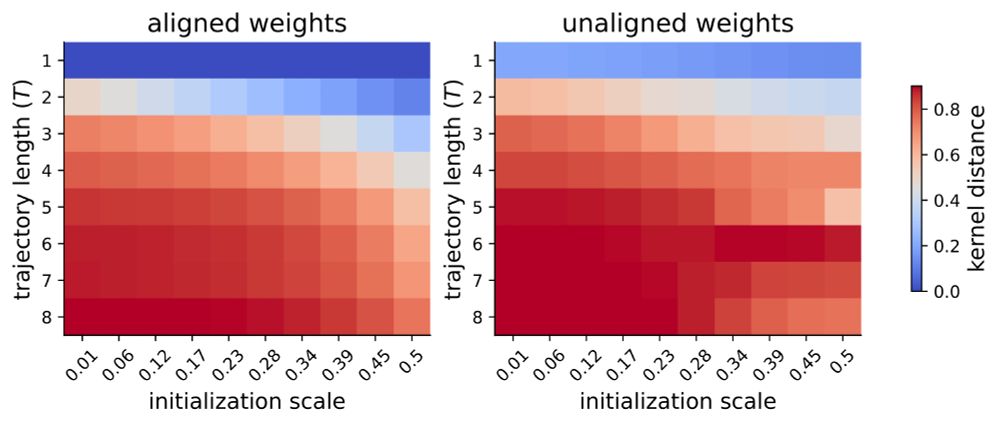
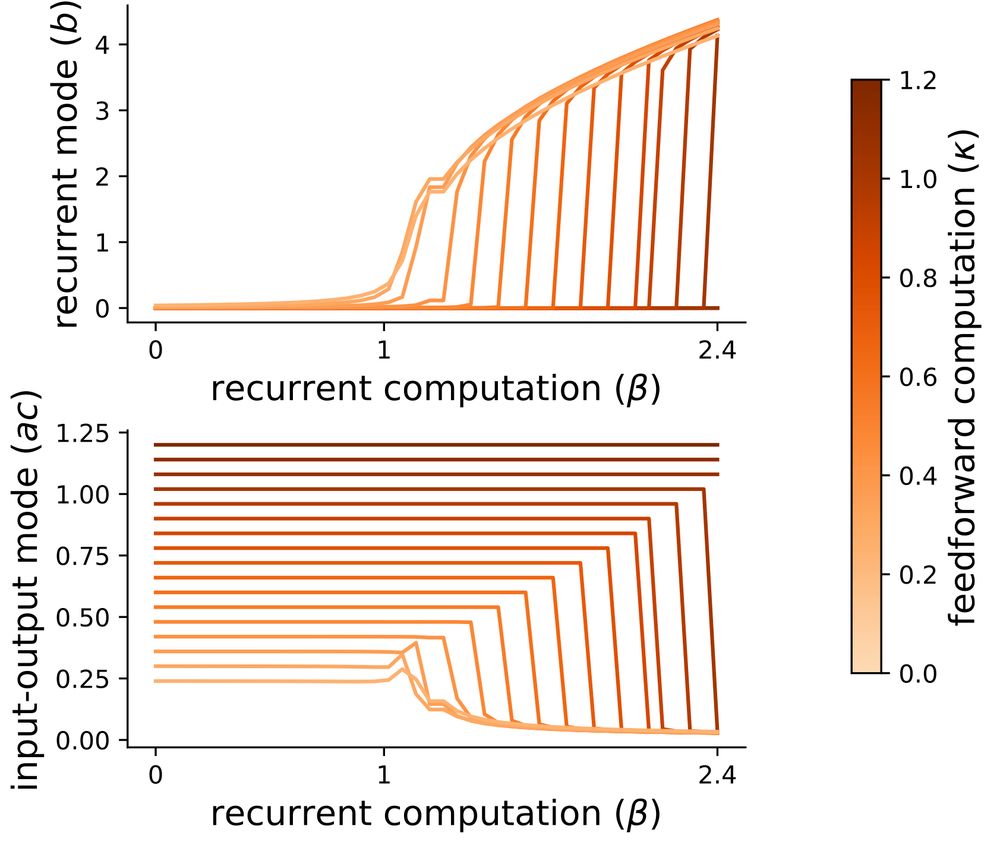
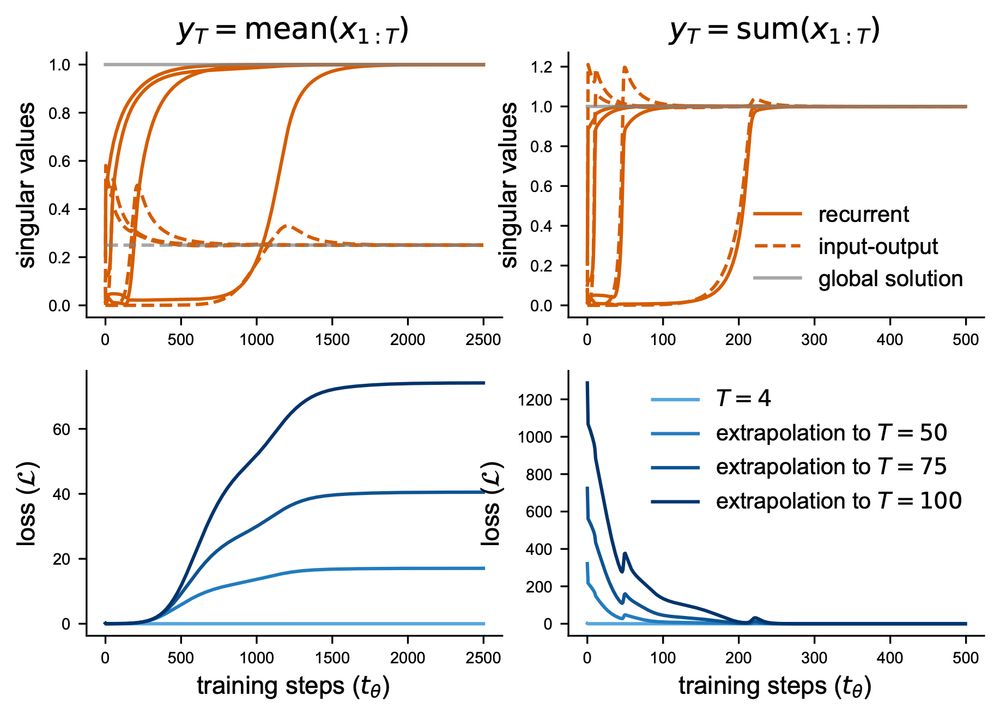
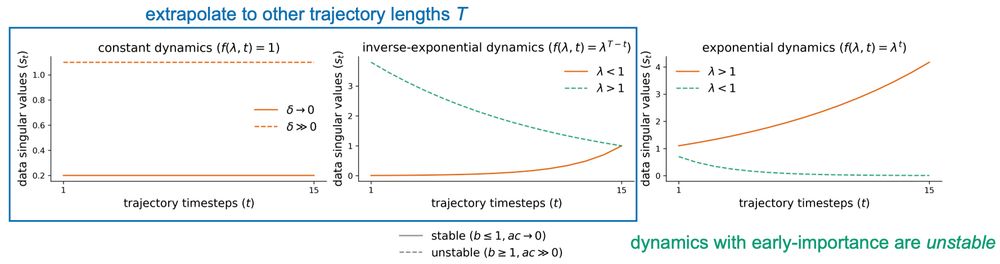
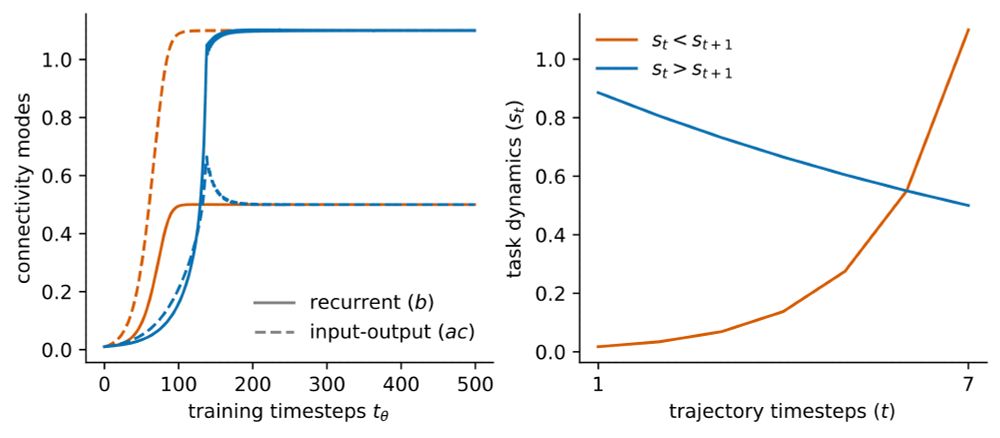
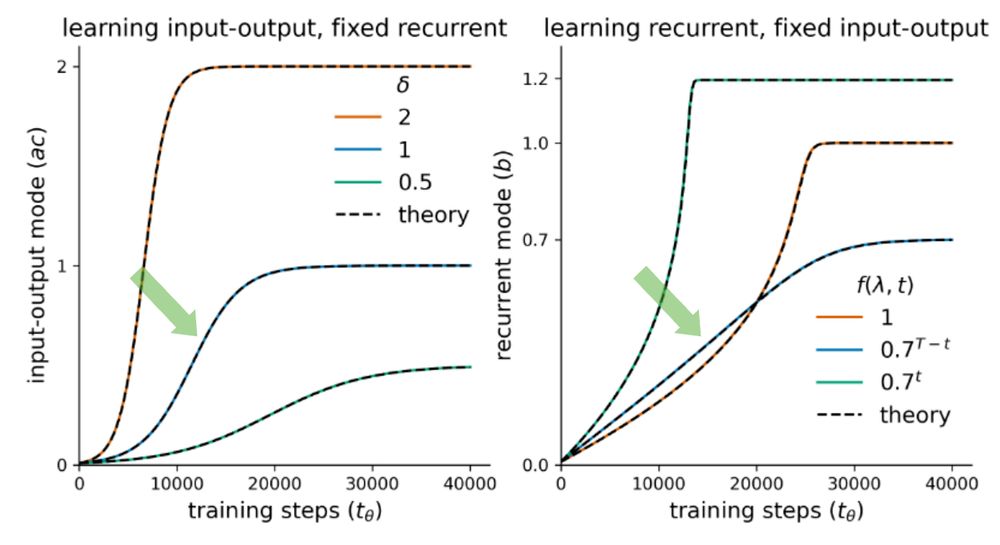
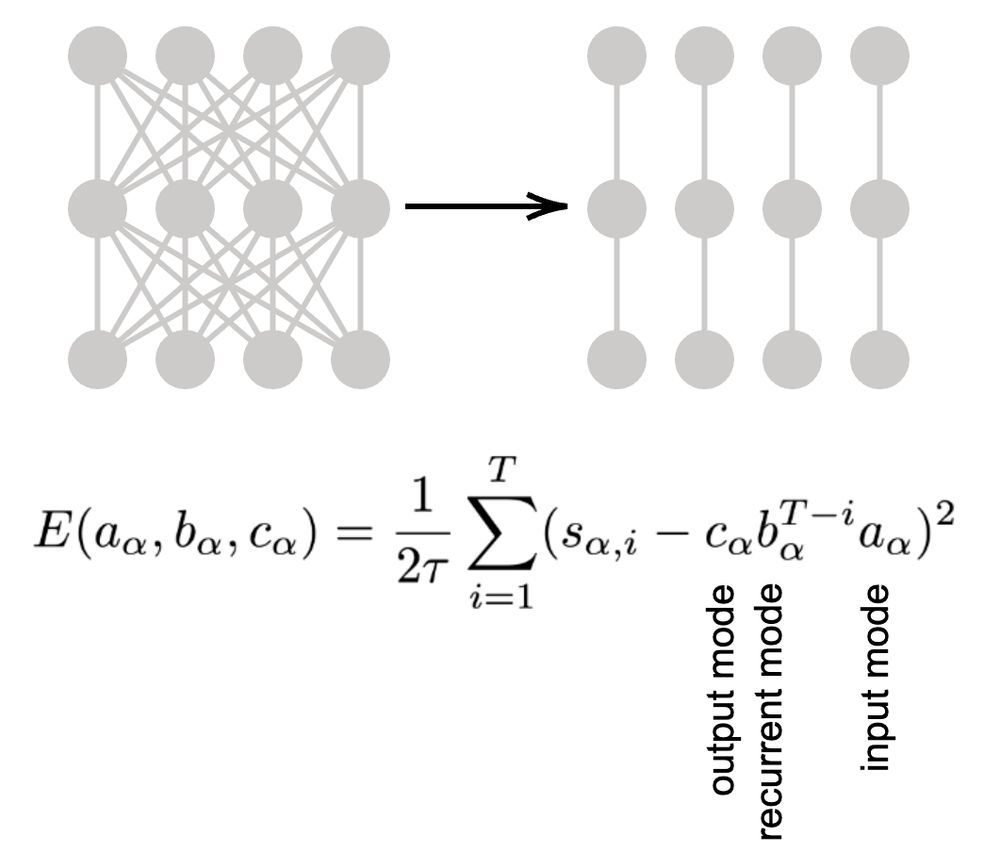
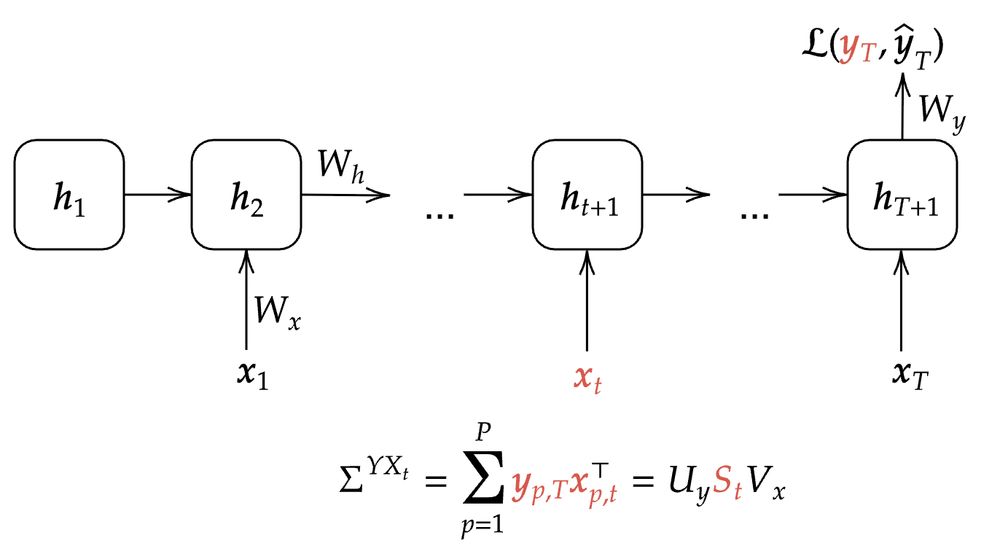
Learning dynamics in linear recurrent neural networks
Recurrent neural networks (RNNs) are powerful models used widely in both machine learning and neuroscience to learn tasks with temporal dependencies and to model neural dynamics. However, despite...
openreview.net
Reposted by Alexandra Proca
Reposted by Alexandra Proca
Alexandra Proca
@aproca.bsky.social
· Nov 22