www.einzigartigwir.de/en/job-offer...
More info below ...

www.einzigartigwir.de/en/job-offer...
More info below ...

Enjoyed seeing so many old friends, Memming Park, Carlos Brody, Wulfram Gerstner, Nicolas Brunel & many others …
Discussed our recent DS foundation models …

Enjoyed seeing so many old friends, Memming Park, Carlos Brody, Wulfram Gerstner, Nicolas Brunel & many others …
Discussed our recent DS foundation models …
(6/6)
(6/6)
(5/6)
(5/6)
#AI
(4/6)
#AI
(4/6)
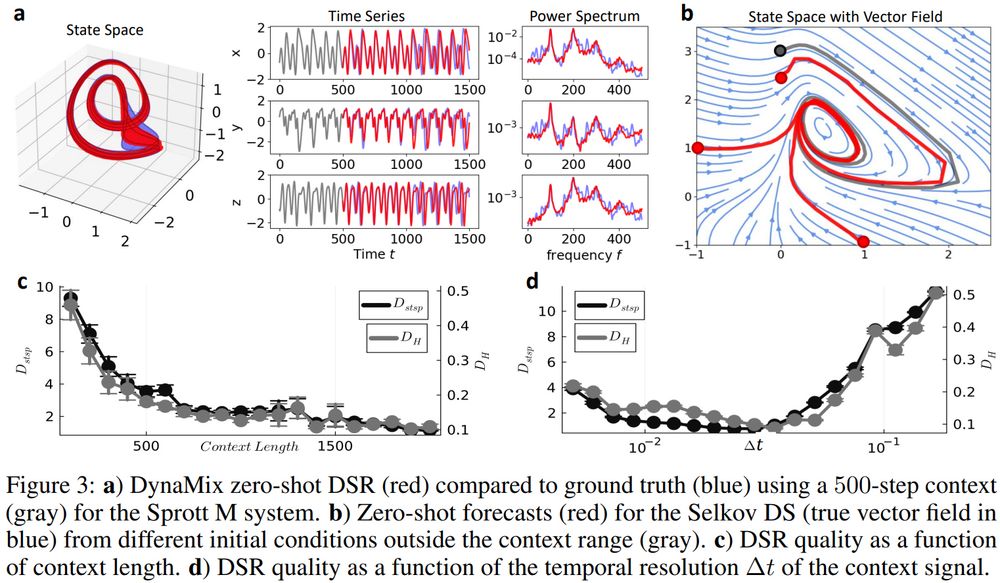
This is surprising, cos DynaMix’ training corpus consists *solely* of simulated limit cycles & chaotic systems, no empirical data at all!
(3/6)
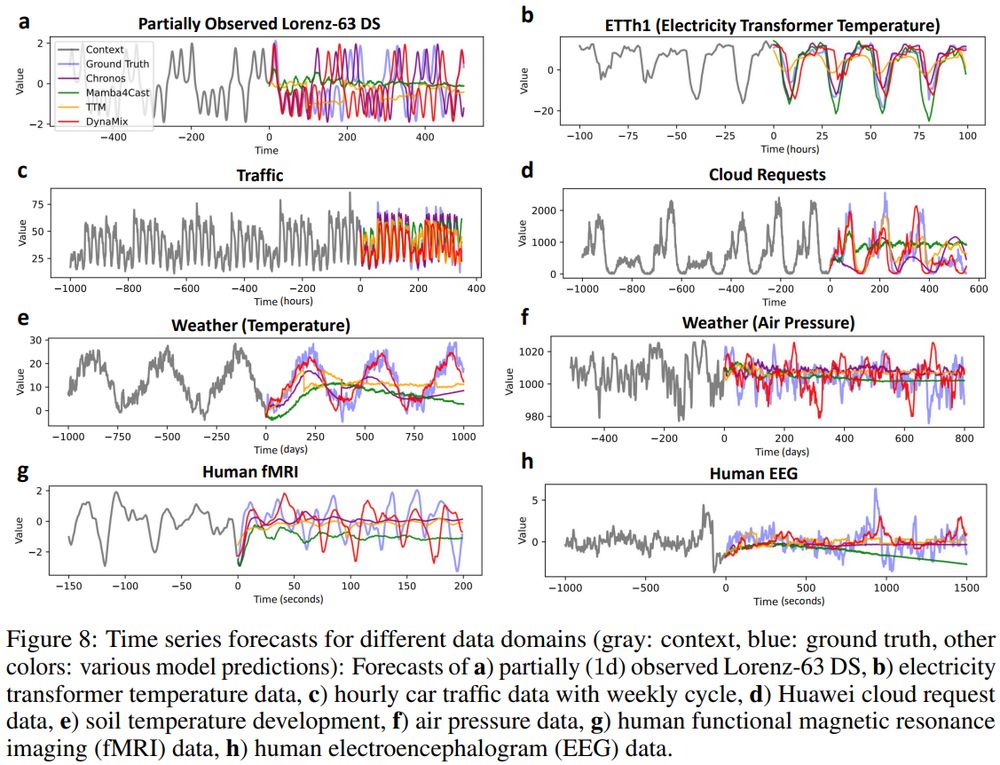
This is surprising, cos DynaMix’ training corpus consists *solely* of simulated limit cycles & chaotic systems, no empirical data at all!
(3/6)
It does so with only 0.1% of the parameters of Chronos & 10x faster inference times than the closest competitor.
(2/6)
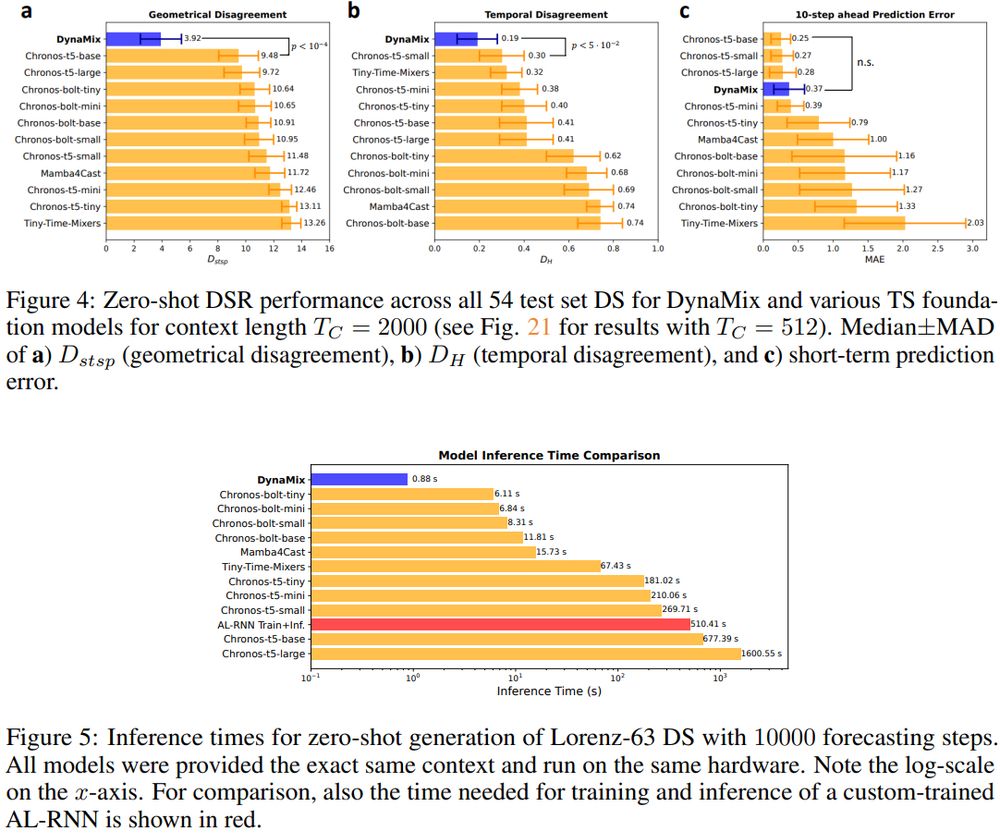
It does so with only 0.1% of the parameters of Chronos & 10x faster inference times than the closest competitor.
(2/6)
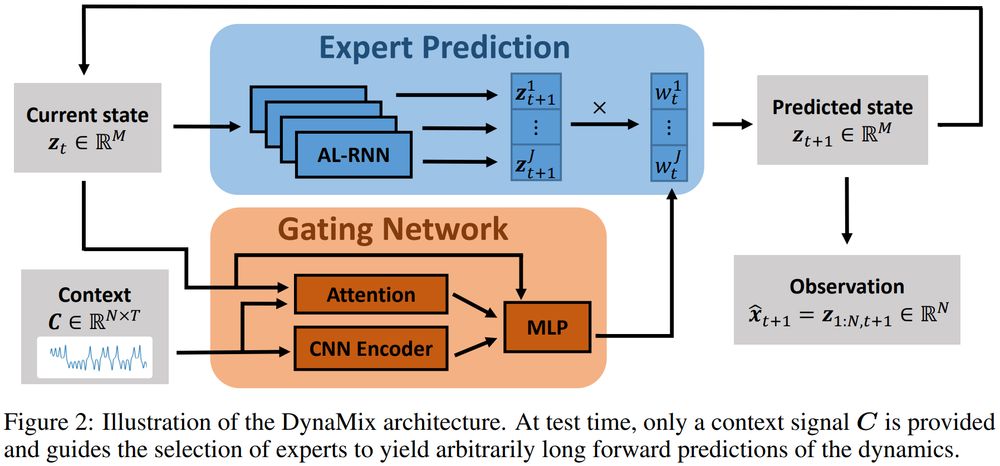
No, they cannot!
But *DynaMix* can, the first TS/DS FM based on principles of DS reconstruction, capturing the long-term evolution of out-of-domain DS: arxiv.org/pdf/2505.131...
(1/6)
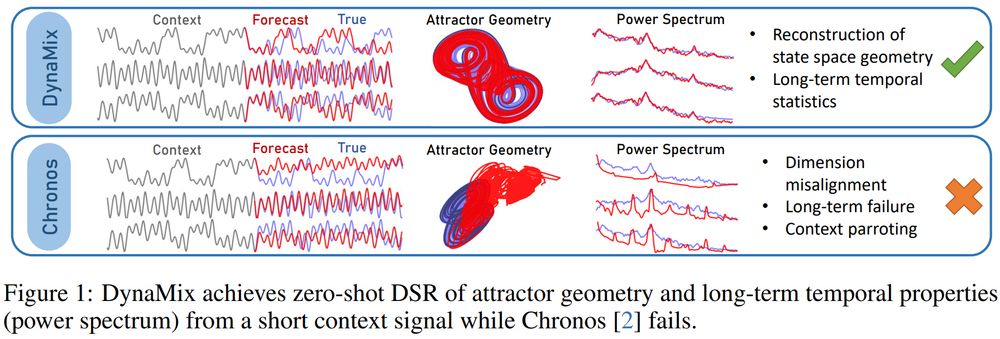
No, they cannot!
But *DynaMix* can, the first TS/DS FM based on principles of DS reconstruction, capturing the long-term evolution of out-of-domain DS: arxiv.org/pdf/2505.131...
(1/6)
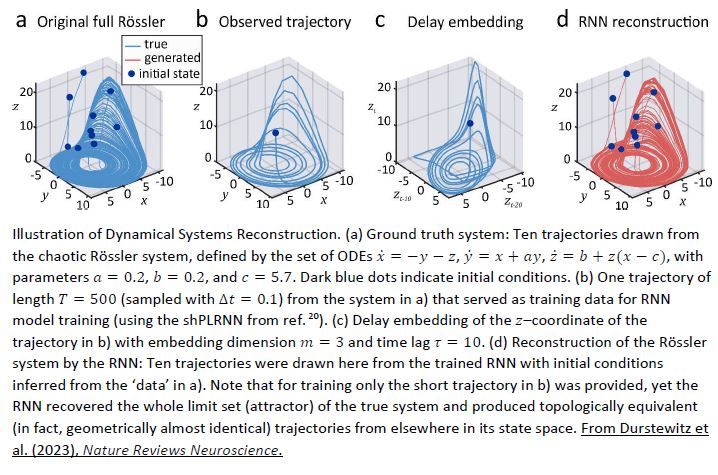
(3/4)
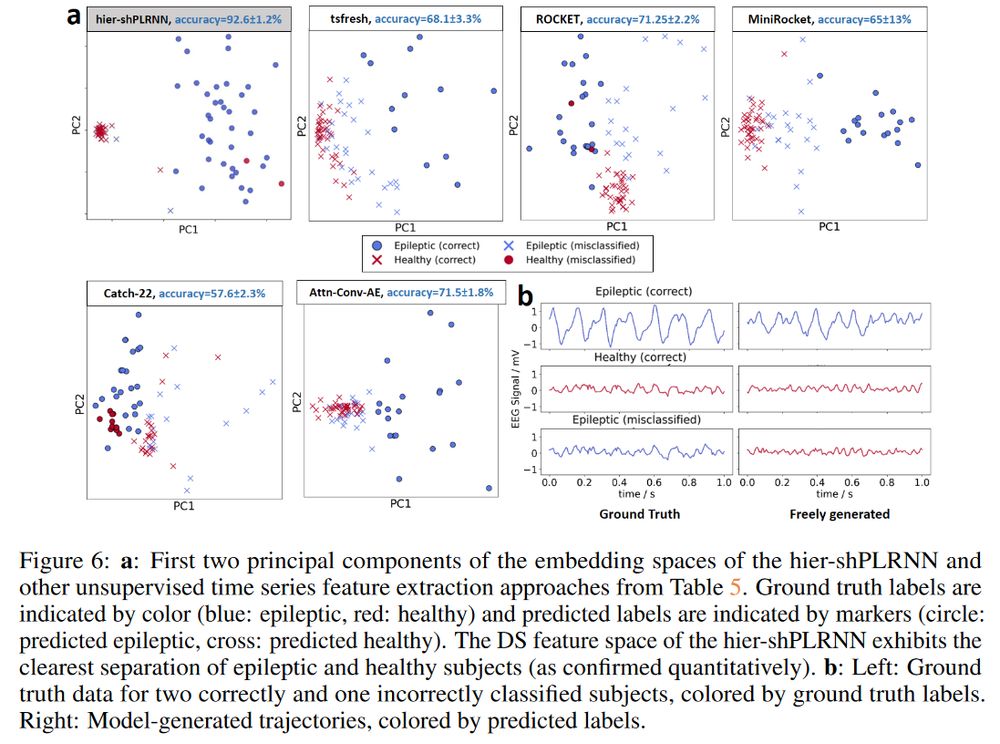
(3/4)
(2/4)
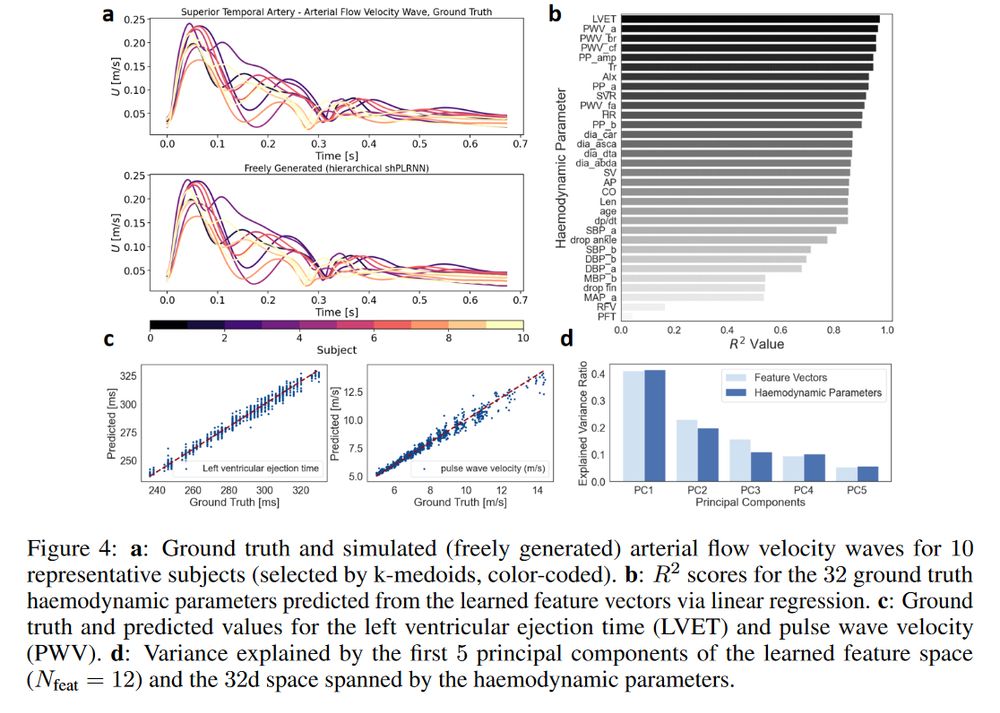
(2/4)
Previous version: arxiv.org/pdf/2410.04814; strongly updated version will be available soon ...
(1/4)
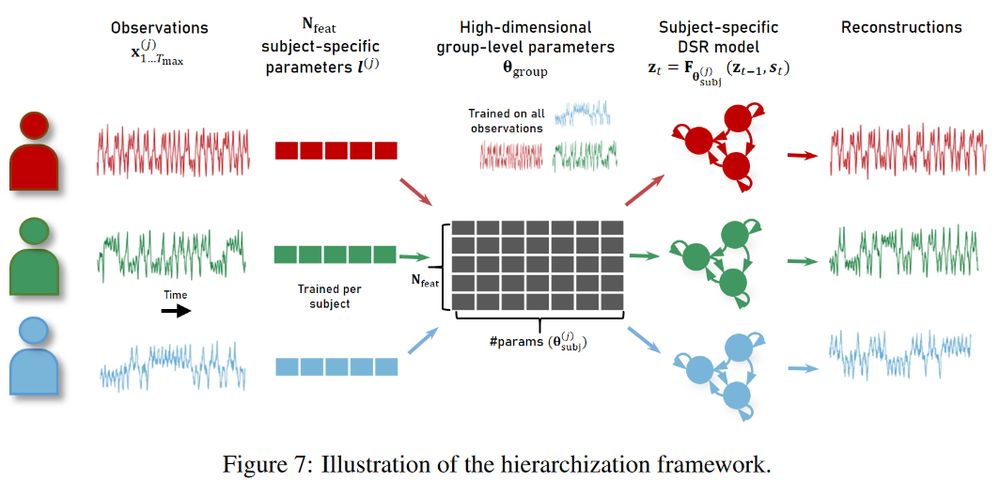
Previous version: arxiv.org/pdf/2410.04814; strongly updated version will be available soon ...
(1/4)
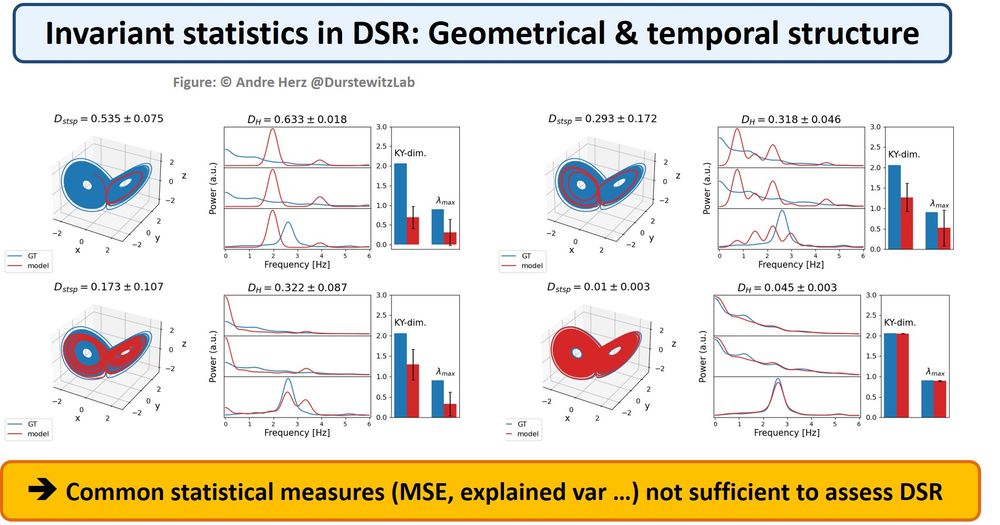



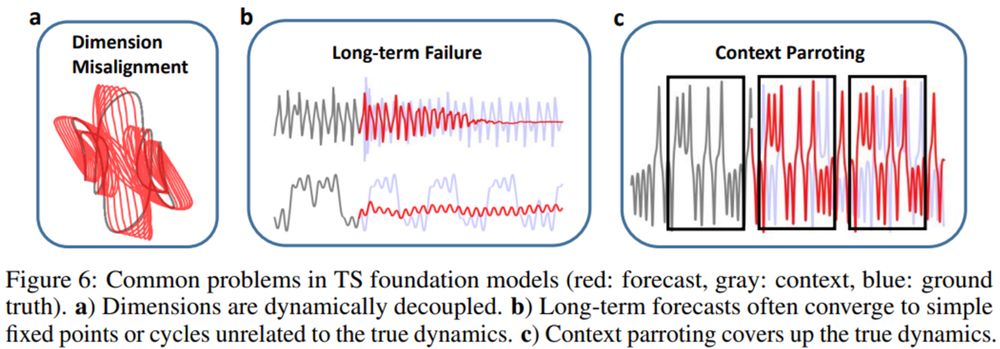
(3/6)

(3/6)
Most other DSR work considers only simulated benchm. & struggles with real data. (2/6)

Most other DSR work considers only simulated benchm. & struggles with real data. (2/6)