
Interested in (deep) learning theory and others.
1) Non-trivial upper bounds on test error for both true and random labels
2) Meaningful distinction between structure-rich and structure-poor datasets
The figures: Binary classification with FCNNs using SGLD using 8k MNIST images

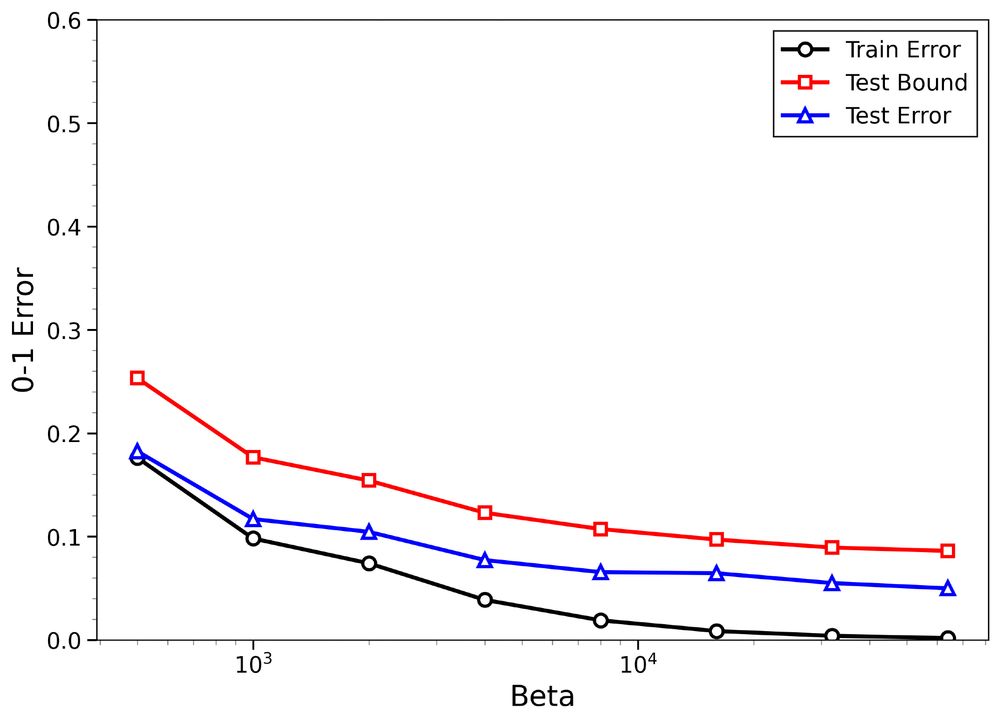
1) Non-trivial upper bounds on test error for both true and random labels
2) Meaningful distinction between structure-rich and structure-poor datasets
The figures: Binary classification with FCNNs using SGLD using 8k MNIST images
📎 Our bounds remain stable under this approximation (in both total variation and W₂ distance).
📎 Our bounds remain stable under this approximation (in both total variation and W₂ distance).
✅ We derive high-probability, data-dependent bounds on the test error for hypotheses sampled from the Gibbs posterior (for the first time in the low-temperature regime β > n).
Sampling from the Gibbs posterior is, however, typically difficult.
✅ We derive high-probability, data-dependent bounds on the test error for hypotheses sampled from the Gibbs posterior (for the first time in the low-temperature regime β > n).
Sampling from the Gibbs posterior is, however, typically difficult.
Here, predictors are sampled from a prescribed probability distribution, allowing us to apply PAC-Bayesian theory to study their generalization properties.

Here, predictors are sampled from a prescribed probability distribution, allowing us to apply PAC-Bayesian theory to study their generalization properties.
arxiv.org/abs/1611.03530

arxiv.org/abs/1611.03530
🔹 Uses blocking methods
🔹 Captures fast-decaying correlations
🔹 Results in tight O(1/n) bounds when decorrelation is fast
Applications:
📊 Covariance operator estimation
🔄 Learning transfer operators for stochastic processes
🔹 Uses blocking methods
🔹 Captures fast-decaying correlations
🔹 Results in tight O(1/n) bounds when decorrelation is fast
Applications:
📊 Covariance operator estimation
🔄 Learning transfer operators for stochastic processes
We propose empirical Bernstein-type concentration bounds for Hilbert space-valued random variables arising from mixing processes.
🧠 Works for both stationary and non-stationary sequences.
We propose empirical Bernstein-type concentration bounds for Hilbert space-valued random variables arising from mixing processes.
🧠 Works for both stationary and non-stationary sequences.
Standard i.i.d. assumptions fail in many learning tasks, especially those involving trajectory data (e.g., molecular dynamics, climate models).
👉 Temporal dependence and slow mixing make it hard to get sharp generalization bounds.
Standard i.i.d. assumptions fail in many learning tasks, especially those involving trajectory data (e.g., molecular dynamics, climate models).
👉 Temporal dependence and slow mixing make it hard to get sharp generalization bounds.
@pontilgroup.bsky.social
arxiv.org/pdf/2406.19861

