
ML, music, generative models, robustness, ML & health
curr & prev affils:
Dalhousie University (CS), Vector Institute, Google Research
"Hide & Seek: Transformer Symmetries Obscure Sharpness & Riemannian Geometry Finds It"
🎓 Marvin F. da Silva, Felix Dangel, and Sageev Oore
🔗 arxiv.org/abs/2505.05409
Questions/comments? 👇we'd love to hear from you!
#ICML2025 #ML #Transformers #Riemannian #Geometry #DeepLearning #Symmetry

"Hide & Seek: Transformer Symmetries Obscure Sharpness & Riemannian Geometry Finds It"
🎓 Marvin F. da Silva, Felix Dangel, and Sageev Oore
🔗 arxiv.org/abs/2505.05409
Questions/comments? 👇we'd love to hear from you!
#ICML2025 #ML #Transformers #Riemannian #Geometry #DeepLearning #Symmetry
Maybe flatness isn’t universal after all—context matters.
Maybe flatness isn’t universal after all—context matters.
Interestingly, flatter is not always better!
Interestingly, flatter is not always better!
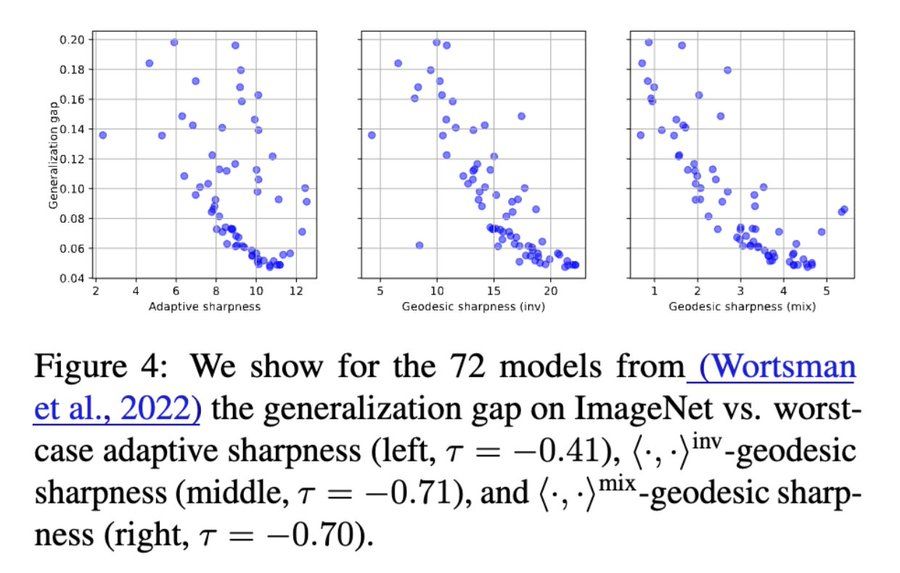
🖼️ Vision Transformers (ImageNet): -0.41 (adaptive sharpness) → -0.71 (geodesic sharpness)
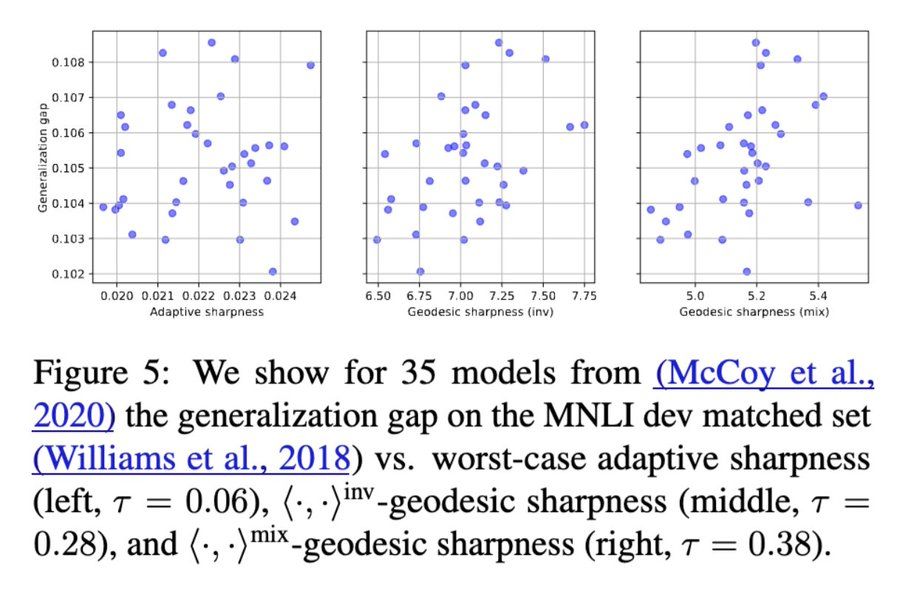
💬 BERT fine-tuned on MNLI: 0.06 (adaptive sharpness) → 0.38 (geodesic sharpness)
🖼️ Vision Transformers (ImageNet): -0.41 (adaptive sharpness) → -0.71 (geodesic sharpness)
💬 BERT fine-tuned on MNLI: 0.06 (adaptive sharpness) → 0.38 (geodesic sharpness)
Perturbations are no longer arbitrary—they respect functional equivalences in transformer weights.
Result: Geodesic sharpness shows clearer, stronger correlations (as measured by the tau correlation coefficient) with generalization. 📈
Perturbations are no longer arbitrary—they respect functional equivalences in transformer weights.
Result: Geodesic sharpness shows clearer, stronger correlations (as measured by the tau correlation coefficient) with generalization. 📈
Whereas traditional sharpness measures are evaluated inside an L^2 ball, we look at a geodesic ball in this symmetry-corrected space, using tools from Riemannian geometry.
Whereas traditional sharpness measures are evaluated inside an L^2 ball, we look at a geodesic ball in this symmetry-corrected space, using tools from Riemannian geometry.
Instead of considering the usual Euclidean metric, we look at metrics invariant both to symmetries of the attention mechanism and to previously studied re-scaling symmetries.
Instead of considering the usual Euclidean metric, we look at metrics invariant both to symmetries of the attention mechanism and to previously studied re-scaling symmetries.
We need to redefine sharpness and measure it not directly in parameter space, but on a symmetry-aware quotient manifold.
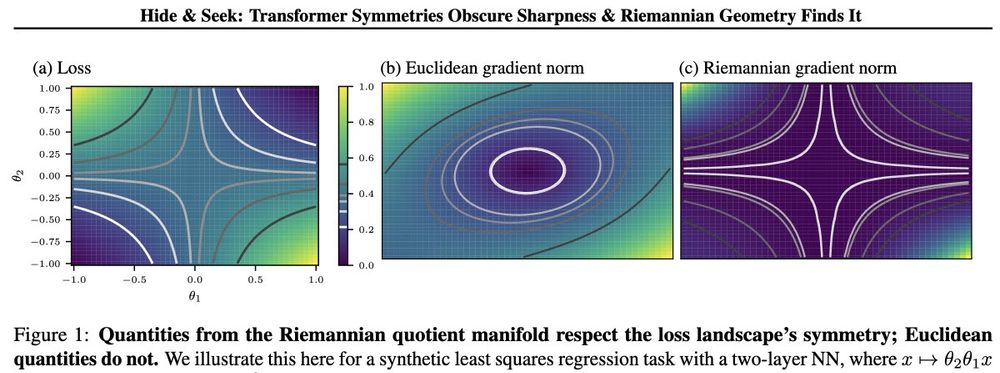
We need to redefine sharpness and measure it not directly in parameter space, but on a symmetry-aware quotient manifold.


Transformers, however, have a richer set of symmetries that aren’t accounted for by traditional adaptive sharpness measures.
Transformers, however, have a richer set of symmetries that aren’t accounted for by traditional adaptive sharpness measures.
Traditional sharpness metrics (like Hessian-based measures or gradient norms) don't account for symmetries, directions in parameter space that don't change the model's output. They measure sharpness along directions that may be irrelevant, making results noisy or meaningless.
Traditional sharpness metrics (like Hessian-based measures or gradient norms) don't account for symmetries, directions in parameter space that don't change the model's output. They measure sharpness along directions that may be irrelevant, making results noisy or meaningless.
Sharpness (flat minima) often predicts how well models generalize. But Andriushchenko et al. (2023) found that transformers consistently break this intuition. Why?
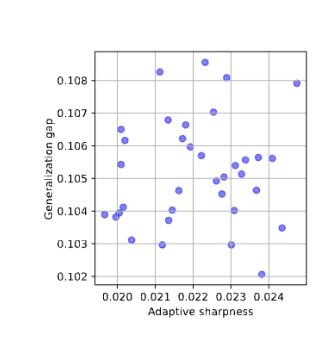
Sharpness (flat minima) often predicts how well models generalize. But Andriushchenko et al. (2023) found that transformers consistently break this intuition. Why?

