Researcher at Google DeepMind
Kiwi🇳🇿 in California🇺🇸
http://stein.ke/



![[Screenshot of an app]
Code Verification
Call customer service at 1-866-4220306 (outside the U.S. call 1-210-677-0065) to retrieve your One-time identification Code .](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiffo5kk6fobzmxoz3dnfwonqj36xejsutsj6wh6kuv4eqwzijh3gi@jpeg)
![def modinv(a, p):
"""Computes inverse of a modulo p i.e. returns b such that (a*b)%p==1"""
u, v = a % p, p
x, y, w, z = 1, 0, 0, 1 # maintain ax+py==u and aw+pz==v
while u != 0: # extended Euclidean algorithm
q, r = v // u, v % u
x, y, w, z = w-qx, z-qy, x, y
u, v = r, u
if v != 1: return None # not invertible
return w % p
def modmatrixinverse(A, p):
"""Computes matrix inverse of A modulo p i.e. returns B s.t. A@B%p==I"""
A = numpy.array(A, dtype=int)
m, n = A.shape
assert m == n, "matrix must be square"
B = numpy.eye(n, dtype=int) # = nxn identity matrix
for i in range(n): # Gaussian elimination
b, j = None, i-1
while b is None:
j += 1
if j >= n: return None # not invertible
b = modinv(A[j,i], p)
if j > i: # swap rows i and j
A[j,:], A[i,:] = A[i,:], A[j,:]
B[j,:], B[i,:] = B[i,:], B[j,:]
A[i,:] = (A[i,:] * b) % p # divide A[i,:] by A[i,i]
B[i,:] = (B[i,:] * b) % p
for j in range(n): # zero out the rest of column i
if j != i:
B[j,:] = (B[j,:] - B[i,:] * A[j,i]) % p
A[j,:] = (A[j,:] - A[i,:] * A[j,i]) % p
return B](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreifpv2rkjmgnwfgoaumjmxgv3gkd3rwufyinjvthca4dzcc2nbntwu@jpeg)

![\textbf{H\"older's inequality from Jensen's inequality:}
\noindent
Let $x,y\in\mathbb{R}^d$ be arbitrary. Let $p,q \in (1,\infty)$ satisfy $\frac1p+\frac1q=1$. Without loss of generality, assume $x_i \ne 0$ for all $i \in [d]$.
Note that $v \mapsto |v|^p$ is convex.
For $i \in [d]$, define $u_i = |x_i|^q/\|x\|_q^q$ and $v_i = x_iy_i/|x_i|^q$. By Jensen's inequality,
\[\left|\frac{\sum_i x_i y_i}{\|x\|_q^q}\right|^p = \left|\sum_i u_i v_i\right|^p \le \sum_i u_i |v_i|^p = \frac{\sum_i |x_i|^{q+p-pq}|y_i|^p}{\|x\|_q^q} = \frac{\|y\|_p^p}{\|x\|_q^q}, \]
which rearranges to \[\left|\sum_i x_i y_i\right| \le \|x\|_q \cdot \|y\|_p.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreicxf5yshu7vcv6j625wl3ulltwhdsgxugxejil247ily2obs7n37i@jpeg)
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?

![\textbf{Jensen's inequality:}
\noindent
Let $x,y\in\mathbb{R}^d$ be arbitrary. Without loss of generality, assume $x_i \ne 0$ for all $i \in [d]$.
For $i \in [d]$, define $p_i = x_i^2/\|x\|^2$ and $v_i = y_i/x_i$. By Jensen's inequality,
\[\left(\frac{\sum_i x_i y_i}{\|x\|^2}\right)^2 = \left(\sum_i p_i v_i\right)^2 \le \sum_i p_i v_i^2 = \frac{\sum_i y_i^2}{\|x\|^2}, \]
which rearranges to \[\sum_i x_i y_i \le \|x\| \cdot \|y\|.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiamyqso2lvlqbm35ryvp7ho7s2zelc4j4e23uefiopg44dj3yzqq4@jpeg)
![\textbf{Sum of squares:}
\noindent
Let $x,y\in\mathbb{R}^d$.
For all $\alpha,\beta>0$,
\[0 \le \| \alpha x - \beta y \|^2 = \alpha^2\|x\|^2 + \beta^2\|y\|^2 -2\alpha\beta\langle x , y \rangle\]
and, hence,
\[\langle x , y \rangle \le \frac{\alpha}{2\beta}\|x\|^2 + \frac{\beta}{2\alpha}\|y\|^2.\]
If $\|x\|=0$ or $\|y\|=0$, clearly $\langle x , y \rangle = 0$. Otherwise, set $\alpha=\|y\|$ and $\beta=\|x\|$ to obtain
\[\langle x , y \rangle \le \frac{\|y\|}{2\|x\|}\|x\|^2 + \frac{\|x\|}{2\|y\|}\|y\|^2 = \|x\| \cdot \| y \|.\]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreid3dwwigb4tczqgxa4hmdmtrzeucppw5ruvkd7tpcrlsc234f6kwi@jpeg)
⟨x,y⟩ ≤ ∥x∥ ∥y∥
Are there any others you know of?
Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution

Then X·Y+W·Z has a standard Laplace distribution.
Similarly, Z·√(X^2+Y^2) has a standard Laplace distribution
E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁

E.g. if you have a bounded query and add Gaussian noise, you can condition the noisy output to also be bounded without any loss in privacy parameters. 😁



But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
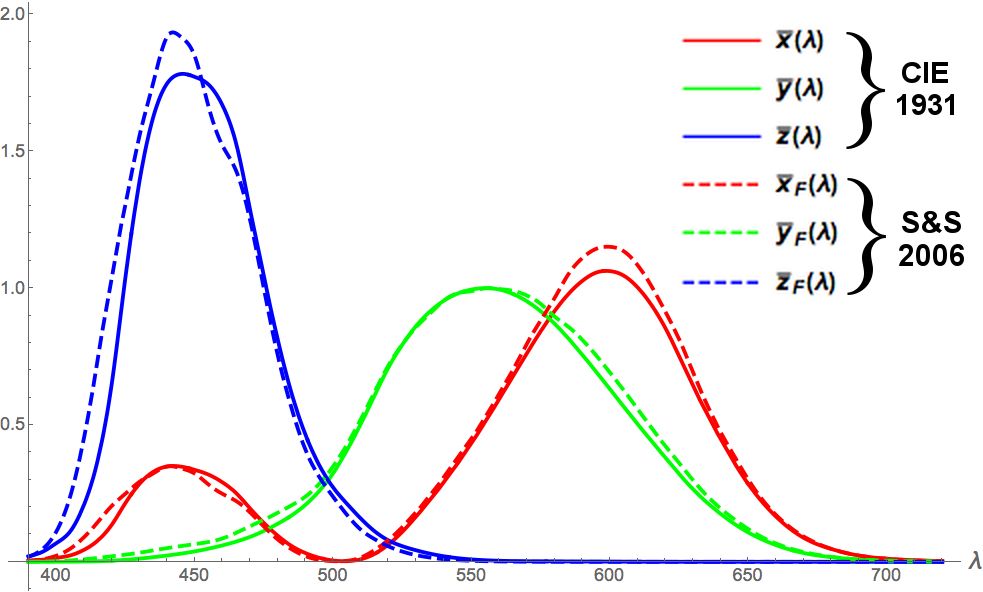
But humans can only perceive a three-dimensional projection of colour (red, green, & blue).
What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.
![Full LaTeX source: https://pastebin.com/mA6KjUJs
\begin{proposition}[Triangle-like inequality for KL divergence]\label{prop:kl-triangle}
Let $P$, $R$, and $Q$ be probability distributions with $P$ being absolutely continuous with respect to $R$ and $R$ being absolutely conotinuous with respect to $Q$.
Let $\kappa \in (1,\infty)$.
Then
\[
\dr{\text{KL}}{P}{Q} \le \frac{\kappa}{\kappa-1} \dr{\text{KL}}{P}{R} + \dr{\kappa}{R}{Q},
\]
where $\dr{\text{KL}}{P}{Q} := \ex{X \gets P}{\log(P(X)/Q(X)}$ denotes the KL divergence and\\$\dr{\kappa}{R}{Q} = \frac{1}{\kappa-1} \log \ex{X \gets R}{(R(X)/Q(X))^{\kappa-1}}$ denotes the R\'enyi divergence of order $\kappa$.
\end{proposition}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreibz3gfiqvyvbld7jgfnb6kzac2j6qrxirofpwrxiv5mpz6j7r6md4@jpeg)
The proof boils down to Holder's inequality.

The proof boils down to Holder's inequality.


The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )


The uniform guarantee is as tight as the pointwise guarantee.
(Alas I couldn't get this proof down to 1 page. 😅 )
And the matrix is lower-triangular, so it's easy to invert.
![LaTeX source: https://pastebin.com/qtw8DPh8
\begin{lemma}[Quotient Rule for Higher Derivatives] ~\\
Let $h(x) := \frac{f(x)}{g(x)}$ with $g(x) \ne 0$. Then, %$h'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$. More generally,
for all $n \in \mathbb{N}$,
\[
\left(\begin{array}{c}
h(x) \\
h'(x) \\
h''(x) \\
h'''(x) \\
\vdots \\
h^{(k)}(x) \\
\vdots \\
h^{(n-1)}(x)
\end{array}\right)
=
\left(\begin{array}{ccccc}
g(x) & 0 & 0 & \cdots & 0 \\
g'(x) & g(x) & 0 & \cdots & 0 \\
g''(x) & 2 g'(x) & g(x) & \cdots & 0 \\
g'''(x) & 3 g''(x) & 3 g'(x) & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & 0 \\
g^{(k)}(x) & {k \choose 1} g^{(k-1)}(x) & {k \choose 2} g^{(k-2)}(x) & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & 0 \\
g^{(n-1)}(x) & {n-1 \choose 1} g^{(n-2)}(x) & {n-1 \choose 2} g^{(n-3)}(x) & \cdots & g(x)
\end{array}\right)^{-1}
\left(\begin{array}{c}
f(x) \\
f'(x) \\
f''(x) \\
f'''(x) \\
\vdots \\
f^{(k)}(x) \\
\vdots \\
f^{(n-1)}(x)
\end{array}\right) .
\]
\end{lemma}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreidykasrfyvrd4w77drvh2wesxkxkqmswvvzom5fzm27p7wb7da7fe@jpeg)
And the matrix is lower-triangular, so it's easy to invert.
doi.org/10.1007/BF02...

doi.org/10.1007/BF02...
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
![creenshot from Google Scholar with the followng text. But no link to the paper.
[CITATION] The value of the definite integral∫∞−∞ eat2+ bt ect+ d dt
LJ Mordell - Quarterly J. of Math, 1920
Save Cite Cited by 35 Related articles](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreif65lvthgv7ln6q6xxgdtf3wrl5sollmu5q6e7i7f2hd7qvyhyreu@jpeg)
If you try looking up Mordell's original paper from 1920, you get nothing: 🙃
en.wikipedia.org/wiki/Logit-n...
![\begin{proposition}[Mean of Logit-Normal Distribution]
For all $\mu\in\mathbb{R}$ and all $\sigma>0$,
\begin{align*}
&\ex{X \gets \mathcal{N}(\mu,\sigma^2)}{\frac{1}{1+e^{-X}}} = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty \frac{1}{1+e^{-(\mu+\sigma x)}} e^{-x^2/2} \mathrm{d}x \\
&= \frac12 + \frac{\sum_{n=1}^\infty e^{-\sigma^2n^2/2} \sinh(n\mu)\tanh(n\sigma^2/2) + \frac{2\pi}{\sigma^2} e^{-(2n-1)^2\pi^2/2\sigma^2} \frac{\sin((2n-1)\pi\mu/\sigma^2)}{\sinh((2n-1)\pi^2/\sigma^2)}}{1 + 2 \sum_{m=1}^\infty e^{-\sigma^2m^2/2} \cosh(m\mu)}
\end{align*}
\end{proposition}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreiah5ittkezmk46nyanv7imc2ha6c6klzuqvh5nj7fx33w5rsl4gxi@jpeg)
en.wikipedia.org/wiki/Logit-n...
![\begin{theorem}
For all $c>1$, \[\frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1}{c+\sin(\theta)} \mathrm{d} \theta = \frac{1}{\sqrt{c^2-1}}.\]
\end{theorem}
\begin{proof}
Clearly
\[\frac{\mathrm{d}}{\mathrm{d}\theta} \left[ \frac{2}{\sqrt{c^2-1}} \tan^{-1}\left(\frac{1 + c \tan (\theta/2)}{\sqrt{c^2-1}}\right) \right] = \frac{1}{c+\sin(\theta)}.\]
The result now follows from the fundamental theorem of calculus.
\end{proof}](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:thfnaqgktdwqbm42radc322i/bafkreih422niyuwsosyjc5yndqxohza3mo5snurp4vofn4g54igvqi3icu@jpeg)


