Scholar

William Gilpin

Videos
H-index: 18

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

texasscience.bsky.social
Kudos to Edoardo Baldini, William Gilpin & Daehyeok Kim on earning Faculty Early Career Development Program (CAREER) Awards from the National Science Foundation!

#NSF #CAREERAwards #EarlyCareerDevelopment #TexasScience @wgilpin.bsky.social @utphysics.bsky.social
cns.utexas.edu/news/accolad...
Three College of Natural Sciences Faculty Win NSF CAREER Awards
3 UT faculty in computer science and physics won an NSF award recognizing their potential to serve as academic role models.
cns.utexas.edu
1 2

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

spintheory.bsky.social
I'm excited to say that one of the most exploratory and thought-provoking papers I've worked on in recent years was just accepted at Physical Review Research.

Preprint here: arxiv.org/abs/2502.21072

#physics #innovation 🧪🦋 @apsphysics.bsky.social
Innovation-exnovation dynamics on trees and trusses
Innovation and its complement exnovation describe the progression of realized possibilities from the past to the future, and the process depends on the structure of the underlying graph. For example, ...
arxiv.org
3 3 21

Reposted by: William Gilpin

Reposted by: William Gilpin

by William Gilpin

Reposted by: William Gilpin

Reposted by: William Gilpin

by William Gilpin

wgilpin.bsky.social
hi david, thank you very much :)
1

by William Gilpin

wgilpin.bsky.social
Paper: doi.org/10.1371/jour...

Code: github.com/williamgilpi...

Explanatory Website & Code demo: williamgilpin.github.io/illotka/demo...
Optimization hardness constrains ecological transients
Author summary Distinct species can serve overlapping functions in complex ecosystems. For example, multiple cyanobacteria species within a microbial mat might serve to fix nitrogen. Here, we show mat...
doi.org
2

by William Gilpin

wgilpin.bsky.social
This work was inspired by amazing recent work on transients by the dynamical systems community: Analogue KSAT solvers, slowdowns in gradient descent during neural network training, and chimera states in coupled oscillators. (12/N)
1 1

by William Gilpin

wgilpin.bsky.social
For the Lotka-Volterra case, optimal coordinates are the right singular vectors of the species interaction matrix. You can experimentally estimate these with O(N) operations using Krylov-style methods: perturb the ecosystem, and see how it reacts. (11/N)
1

by William Gilpin

wgilpin.bsky.social
This variation influences how we reduce the dimensionality of biological time series. With non-reciprocal interactions (like predator prey), PCA won’t always separate timescales. The optimal dimensionality-reducing variables (“ecomodes”) should precondition the linear problem (10/N)
1 1

by William Gilpin

wgilpin.bsky.social
As a consequence of ill-conditioning, large ecosystems become excitable: small changes cause huge differences in how they approach equilibrium. Using the FLI, a metric invented by astrophysicists to study planetary orbits, we see caustics indicating variation in solve path (9/N)
1

by William Gilpin

wgilpin.bsky.social
How would hard optimization problems arise in nature? I used genetic algorithms to evolve ecosystems towards supporting more biodiversity, and they became more ill-conditioned—and thus more prone to supertransients. (8/N)
1

by William Gilpin

wgilpin.bsky.social
So ill-conditioning isn’t just something numerical analysts care about. It’s a physical property that measures computational complexity, which translates to super long equilibration times in large biological networks with trophic overlap (7/N)
1 1

by William Gilpin

wgilpin.bsky.social
More precisely: the expected equilibration time of a random Lotka-Volterra system scales with the condition number of the species interaction matrix. The scaling matches the expected scaling of the solvers that your computer uses to do linear regression (6/N)
1 1

by William Gilpin

wgilpin.bsky.social
We can think of ecological dynamics as an analogue constraint satisfaction problem. As the problem becomes more ill-conditioned, the ODEs describing the system take longer to “solve” the problem of who survives and who goes extinct (5/N)
1 2

by William Gilpin

wgilpin.bsky.social
But is equilibrium even relevant? In high dimensions, stable fixed points might not be reachable in finite time. Supertransients due to unstable solutions that trap dynamics for increasingly long durations. E.g, pipe turbulence is supertransient (laminar flow is globally stable) (4/N)
1 1

by William Gilpin

wgilpin.bsky.social
Dynamical systems are linear near fixed points, so May used random matrix theory to show large random ecosystems are usually unstable. The biodiversity we see in the real world requires finer-tuned structure from selection, niches, et al. that recover stability (3/N)
1 1

by William Gilpin

wgilpin.bsky.social
A celebrated result in mathematical biology is Robert May’s “stability vs complexity” tradeoff. In large biological networks, we can’t possibly measure all N^2 interactions among N species, genes, neurons, etc. What is our null hypothesis for their behavior? (2/N)
1 1

by William Gilpin

wgilpin.bsky.social
Does stability matter in biology? My article on the cover of this month’s @PLOSCompBiol explores how large ecosystems develop supertransients, a manifestation of computational hardness (1/N)

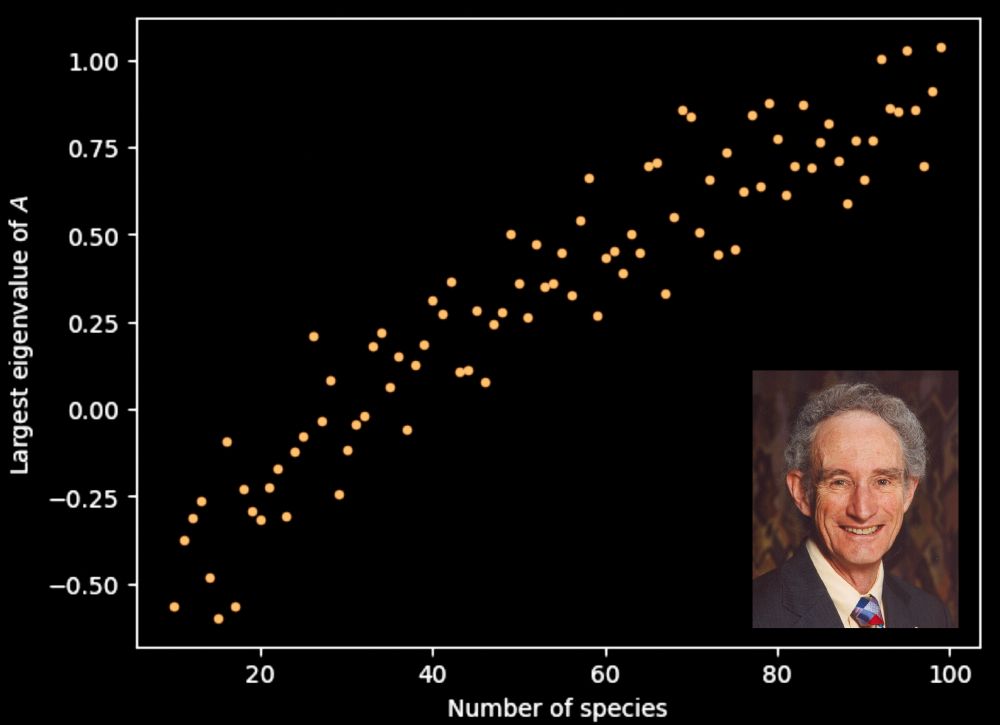
doi.org/10.1371/jour...
1 3 21

by William Gilpin

wgilpin.bsky.social
Code here: github.com/abao1999/panda

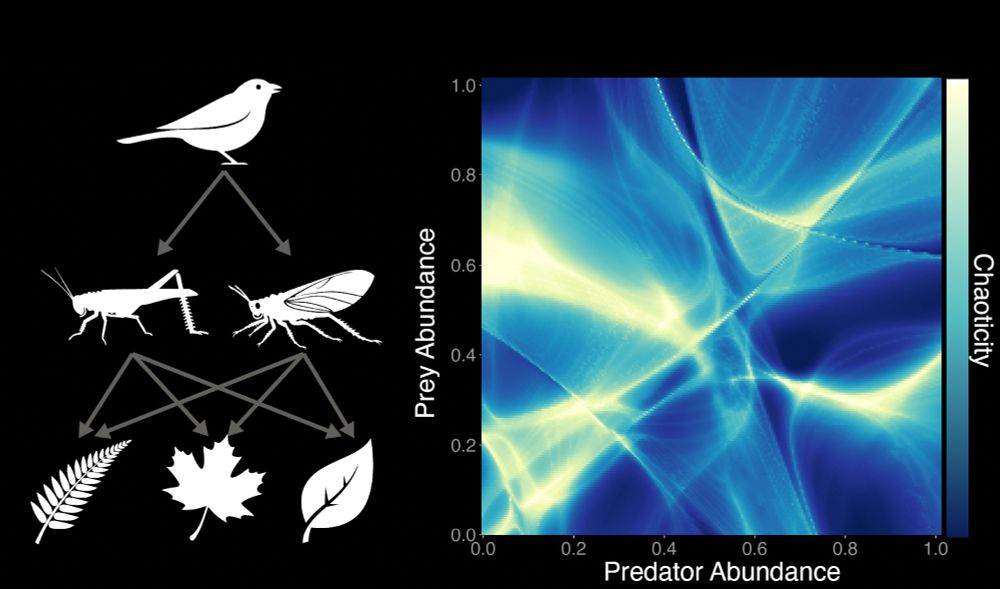
Paper here: arxiv.org/abs/2505.13755

Study lead by Jeff Lai and Anthony Bao
GitHub - abao1999/panda: Patched Attention for Nonlinear Dynamics
Patched Attention for Nonlinear Dynamics. Contribute to abao1999/panda development by creating an account on GitHub.
github.com
2

References

Fields & subjects

Updated 1m