
(Flipping heck I’d erased short tweets from my memory. What old hell is this character clock?)
(Flipping heck I’d erased short tweets from my memory. What old hell is this character clock?)

@zackpolanski.bsky.social
#BoldPolitics
@zackpolanski.bsky.social
#BoldPolitics
You said there are 69,000 #LongCovidKids which is wrong. Please see the chart below.
The number of children suffering DOUBLED Mar '23-Mar'24. Despite this alarming rise in the number of sick chn the govt. are not bothering to collect any more data 🤯
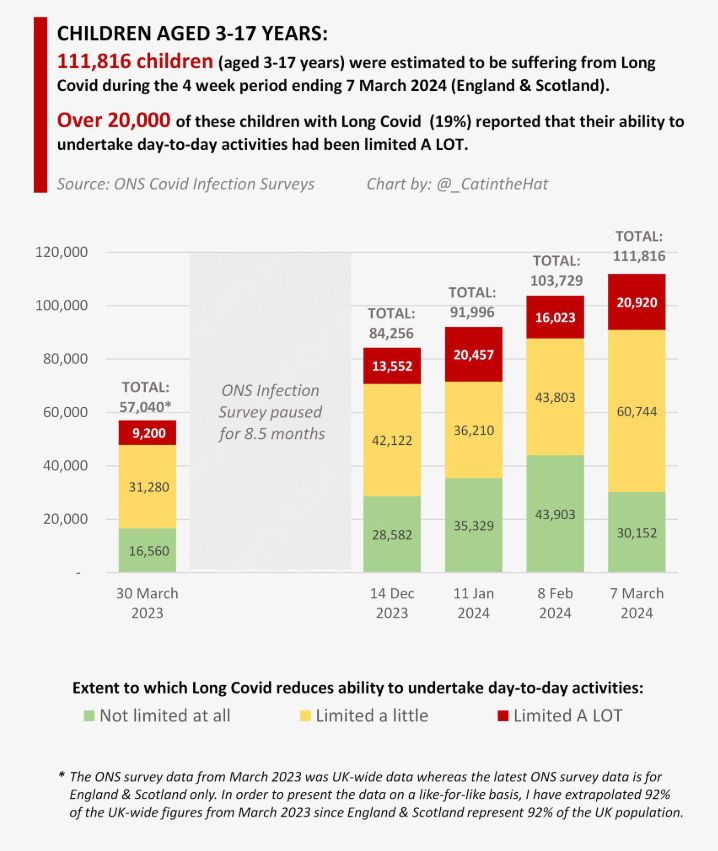
You said there are 69,000 #LongCovidKids which is wrong. Please see the chart below.
The number of children suffering DOUBLED Mar '23-Mar'24. Despite this alarming rise in the number of sick chn the govt. are not bothering to collect any more data 🤯
I suspect the latter is correct.
I didn’t like the Python it generated behind the scenes for the first answer.
I suspect the latter is correct.
I didn’t like the Python it generated behind the scenes for the first answer.
The probability of being present for exactly 12 out of 13 deaths while working only 20% of shifts is approximately 0.0000000426 (or 4.26 in 100 million). This is an extremely unlikely event
The probability of being present for exactly 12 out of 13 deaths while working only 20% of shifts is approximately 0.0000000426 (or 4.26 in 100 million). This is an extremely unlikely event
“Statistically, what are the chances of being present for 12 out of 13 deaths if you only worked 20% of shifts. This is a genuine question. I don't know the answer.”
“Statistically, what are the chances of being present for 12 out of 13 deaths if you only worked 20% of shifts. This is a genuine question. I don't know the answer.”
This is an extraordinarily rare event. “

This is an extraordinarily rare event. “






