This reveals a continuum of environment-objective pairs consistent with behavior. Inverse RL / IOC typically lies at one end of this continuum.

This reveals a continuum of environment-objective pairs consistent with behavior. Inverse RL / IOC typically lies at one end of this continuum.
1. Infer closed-loop parameters (which can be done efficiently with SSM methods ✅)
2. Derive equations relating the parameters of interest in setting the closed-loop dynamics.
See our paper (also on arXiv, link above) for details!
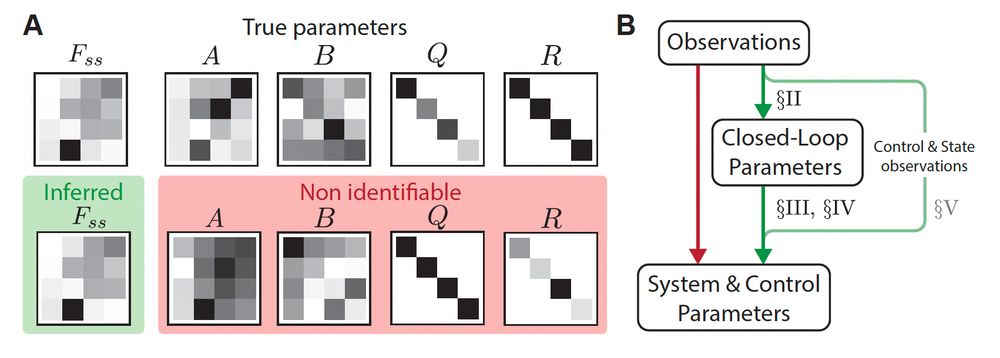
1. Infer closed-loop parameters (which can be done efficiently with SSM methods ✅)
2. Derive equations relating the parameters of interest in setting the closed-loop dynamics.
See our paper (also on arXiv, link above) for details!
A year ago, I was presenting our work at IEEE CDC on solving this problem for stochastic LQR.
arxiv.org/abs/2502.15014
Short 🧵 on the results, and how I think about them a year later.

A year ago, I was presenting our work at IEEE CDC on solving this problem for stochastic LQR.
arxiv.org/abs/2502.15014
Short 🧵 on the results, and how I think about them a year later.

CLDS leverages conditions to approximate the full nonlinear dynamics with locally linear LDSs, bridging the benefits of linear and nonlinear models. [3/5]

CLDS leverages conditions to approximate the full nonlinear dynamics with locally linear LDSs, bridging the benefits of linear and nonlinear models. [3/5]

