Assuming known environments or costs is reasonable in engineered systems, but maybe less so for intelligent agents in complex worlds.

A year later, I see this as clarifying how unobserved objectives and dynamics interact to produce a continuum of explanations, and which perturbations are needed.

One of my favorite equations, after assumptions, details how the system dynamics (A) and control cost (Q) interact with the closed-loop dynamics (F).

This reveals a continuum of environment-objective pairs consistent with behavior. Inverse RL / IOC typically lies at one end of this continuum.

We show that the joint problem boils down to two steps:
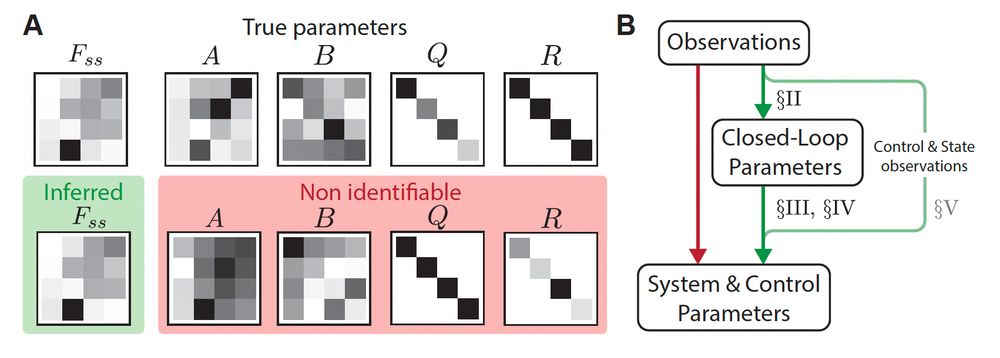
1. Infer closed-loop parameters (which can be done efficiently with SSM methods ✅)
2. Derive equations relating the parameters of interest in setting the closed-loop dynamics.

See our paper (also on arXiv, link above) for details!

Inferring both the system dynamics *and* the control objective from partial observations is inherently ill-posed. Characterizing the exact (non-)identifiability and identifying how to perform inference was the challenge!

This was a theory project spearheading a longer program on neural substrates of cognitive control, with the amazing Juncal Arbelaiz and Harrison Ritz (@hritz.bsky.social), and with great guidance from Nathaniel Daw (@nathanieldaw.bsky.social), Jon Cohen and Jonathan Pillow (@jpillowtime.bsky.social)

In all, CLDS bridges classic LDS and modern nonlinear models:
- Interpretable: linear dynamics conditioned on task variables
- Expressive: parameters vary nonlinearly over conditions
- Efficient: closed-form and fast inference, and shares statistical power across conditions. [6/6]

We demonstrated CLDS on a range of synthetic tasks and datasets, showing how to link dynamical structure to behaviorally relevant variables in a transparent way. [5/6]

Because CLDS is linear in x given u and uses GP priors over u, we have:
✅ Exact latent state inference with Kalman filtering/smoothing;
✅ Tractable Bayesian learning via closed-form EM updates using “conditionally linear regression”, a trick in a basis-function space. [4/5]

CLDS = linear dynamical system in latent state (x), whose coefficients depend nonlinearly on task conditions (u) through Gaussian processes (GP)

CLDS leverages conditions to approximate the full nonlinear dynamics with locally linear LDSs, bridging the benefits of linear and nonlinear models. [3/5]

This is joint work with amazing collaborators: Amin Nejatbakhsh (@aminejat.bsky.social), David Lipshutz (
@lipshutz.bsky.social), Jonathan Pillow (@jpillowtime.bsky.social), and Alex Williams (@itsneuronal.bsky.social).

🔗 OpenReview: openreview.net/forum?id=xgm...
🖥️ Code: github.com/neurostatsla...